Задача 1: В связном графе степени всех вершин чётны. Маляр садится в одну из вершин и красит рёбра в розовый цвет, передвигаясь по ним. Ходить по уже покрашенному ребру он не может, а когда попадает в вершину, из которой не может выйти, заканчивает свою работу. Докажите, что это та самая вершина, с которой он начал.

Задача 2: Оказалось, что маляр покрасил не весь граф. Докажите, что он мог бы покрасить больше рёбер, чем покрасил.

Задача 3: [Теорема 1] Дан связный граф. Докажите, что

а) если в нем нашелся эйлеров цикл (проходящий по каждому ребру ровно по одному разу), то все его вершины имеют чётную степень;

б) если все вершины имеют чётную степень, то в графе существует эйлеров цикл.

Задача 4: [Теорема 2] В связном графе существует эйлеров путь (проходящий по каждому ребру ровно по одному разу, но не обязательно замкнутый) тогда и только тогда, когда не более двух вершин графа имеют нечётную степень.

Задача 5: а) Можно ли из проволоки длины 12 см сложить каркас кубика с ребром 1 см?

б) На какое наименьшее число частей надо разрезать эту проволоку, чтобы из них можно было сложить такой кубик?

Задача 6: На занятии 20 школьников решили каждый по 6 задач, причём каждая задача была решена ровно двумя школьниками. Докажите, что можно организовать разбор всех задач так, чтобы каждый школьник рассказал ровно по 3 задачи.

Задача 7: Город в плане выглядит как квадрат 3 × 3, каждая сторона квар-та-ла-квад-ра-ти-ка – участок улицы длиной 100,м (включая внешний контур квадрата). Какой наименьший путь придется проделать паровому катку, чтобы заасфальтировать все улицы?

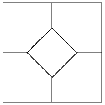
Задача 8: Поле разбито межами на несколько участков (см. рисунок). Землемер захотел, не выходя за пределы поля, пройти по нему так, чтобы пересечь каждую межу ровно один раз. Удастся ли ему это?