 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Индукция-2 | Убрать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2001 г, 7 класс. Индукция-2 |
|
|
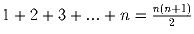 ;
;Задача 2: Докажите, что 1 • 1! + 2 • 2! + … + n • n! = (n + 1)! – 1. Задача 3: На сколько частей делят плоскость n прямых, среди которых нет параллельных и никакие три не пересекаются в одной точке? (Такие прямые называют прямыми «общего положения») Решение:
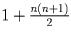 .
Задача 4:
Докажите, что n³ + (n + 1)³ + (n + 2)³ делится на 9 при всех натуральных n.
.
Задача 4:
Докажите, что n³ + (n + 1)³ + (n + 2)³ делится на 9 при всех натуральных n.Задача 5: Докажите, что 6n + 1 делится на 7 при всех нечётных n.
Задача 6: Докажите, что 3n – 1 делится на 8 при чётных n и дает остаток 2 при делении на 8 при нечётных n.
Задача 7: Докажите, что 4n – 3n – 1 делится на 9 при всех натуральных n.
Задача 8: Докажите, что 2n > 2n + 1 при всех натуральных n > 2.
Задача 9: Докажите, что 2n > 8n – 17 при всех натуральных n.
Задача 10: Докажите, что n! > 2n при всех натуральных n ≥ 4. Решение: База n = 4 проверяется непосредственно. Переход: (n + 1)! = (n + 1)n! > 2n(n + 1) > 2 • 2n = 2n + 1.
Задача 11: Докажите, что число, состоящее из 243 единиц, делится на 243. (243 = 35)
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Индукция-2 | Убрать решения |