 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Тест по комбинаторике | Убрать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2001 г, 7 класс. Тест по комбинаторике |
|
|
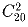 ?
?Задача 2: Чему равно
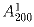 ?
?Задача 3: Известно, что
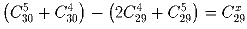 .
Чему может быть равен x?
.
Чему может быть равен x?Задача 4: Известно, что
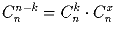 .
Чему может быть равен x? (выразите x через n и k)
Решение:
x = 0 или x = n
.
Чему может быть равен x? (выразите x через n и k)
Решение:
x = 0 или x = nЗадача 5: Известно, что
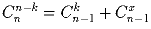 .
Чему может быть равен x? (выразите x через n и k)
Решение:
x = k – 1 или x = n – k
Задача 6:
Вычислите
.
Чему может быть равен x? (выразите x через n и k)
Решение:
x = k – 1 или x = n – k
Задача 6:
Вычислите 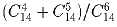 .
Решение:
1
.
Решение:
1Задача 7: Выразите
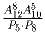 через
через 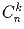 .
Решение:
.
Решение:
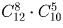 .
Задача 8:
Сколько различных чисел можно составить из цифр
1, 2, 3,…9 (каждая цифра используется ровно один раз)
таких, чтобы никакие две нечётные цифры не стояли рядом?
Решение:
5! • 4!
.
Задача 8:
Сколько различных чисел можно составить из цифр
1, 2, 3,…9 (каждая цифра используется ровно один раз)
таких, чтобы никакие две нечётные цифры не стояли рядом?
Решение:
5! • 4!Задача 9: В группе 18 мальчиков и 2 девочки. Сколько способов выбрать 10 человек для работы в столовой, если хоть одна девочка должна работать? Решение:
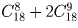 .
.Задача 10: В классе, в котором учатся Петя и Ваня – 17 человек. Сколькими способами можно выбрать из класса команду для ЧГК (6 человек) так, чтобы Петя и Ваня не входили в команду одновременно? Решение:
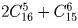 .
.Задача 11: Вычислите наибольший коэффициент в выражении (1 + 2x)5 Решение: 80
Задача 12: План города имеет схему, изображенную на рисунке. На всех улицах введено одностороннее движение: можно ехать только «вправо» или «вверх». Сколько есть разных маршрутов, ведущих из точки A в точку B?
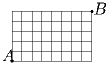
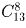 .
.Задача 13: Сколькими способами можно разбить 24 школьников на две команды, в одной из которых – 15 человек, а в другой – 9 человек? Решение:
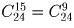 .
.Задача 14: Сколькими способами можно разбить 24 школьников на две команды по 12 человек? Решение:
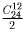 Задача 15:
Сколькими способами можно разбить 24 школьников на четыре команды
по 6 человек?
Решение:
Задача 15:
Сколькими способами можно разбить 24 школьников на четыре команды
по 6 человек?
Решение:
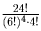 .
.
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Тест по комбинаторике | Убрать решения |