Задача 1:
Найдите площади многоугольников, изображённых на рисунке
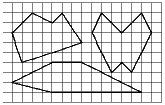
Задача 2:
Нарисуйте треугольник площади ½, у которого
все стороны больше 5, а вершины лежат в узлах сетки.
Решение:
Поскольку в формуле Пика для этого треугольника n ≥ 3
(вершины лежат в узлах сетки), внутри треуголька и на сторонах
(кроме вершин) целых точек нет. Например, годится треугольник,
вершины которого находятся в точках (0,0), (6,1), (5,2).
Задача 3:
Можно ли квадрат 50 × 50 разбить на 15 одинаковых многоугольников с
вершинами в узлах сетки?
Решение:
Нет. По формуле Пика площадь образовавшихся частей должна быть целой или
полуцелой,
а она равна
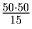
.
Задача 4:
Замкнутая несамопересекающаяся ломаная идет по линиям
сетки и проходит по одному разу через все узлы клетчатого квадрата
7 × 7. Найдите площадь фигуры, ограниченной этой ломаной.
Решение:
Поскольку ломаная проходит через все узлы, внутри узлов нет.
Поскольку на границе лежит 64 точки, то площадь фигуры,
ограниченной ломаной
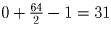
.
Задача 5:
Пусть A и B два узла клетчатой бумаги, из которых, второй на p клеток
правее и на q клеток выше первого. Чему равно расстояние от прямой AB до
ближайшего к ней узла, не лежащего на этой прямой?
Решение:
Пусть C – ближайшая к AB точка.
На отрезке AB лежит НОД (p,q) + 1 точек (считая концы). Внутри
треугольника ABC и на сторонах AC и BC точек нет (так как если бы
такая точка нашлась, то она была бы ближе к прямой AB, чем C).
Не забыв про точку C, видим, что по формуле Пика площадь
треугольника ABC равна
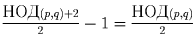
.
Поскольку
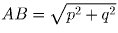
, высота треугольника ABC вычисляется
по формуле
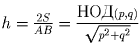
.



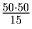 .
.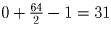 .
Задача 5:
Пусть A и B два узла клетчатой бумаги, из которых, второй на p клеток
правее и на q клеток выше первого. Чему равно расстояние от прямой AB до
ближайшего к ней узла, не лежащего на этой прямой?
Решение:
Пусть C – ближайшая к AB точка.
На отрезке AB лежит НОД (p,q) + 1 точек (считая концы). Внутри
треугольника ABC и на сторонах AC и BC точек нет (так как если бы
такая точка нашлась, то она была бы ближе к прямой AB, чем C).
Не забыв про точку C, видим, что по формуле Пика площадь
треугольника ABC равна
.
Задача 5:
Пусть A и B два узла клетчатой бумаги, из которых, второй на p клеток
правее и на q клеток выше первого. Чему равно расстояние от прямой AB до
ближайшего к ней узла, не лежащего на этой прямой?
Решение:
Пусть C – ближайшая к AB точка.
На отрезке AB лежит НОД (p,q) + 1 точек (считая концы). Внутри
треугольника ABC и на сторонах AC и BC точек нет (так как если бы
такая точка нашлась, то она была бы ближе к прямой AB, чем C).
Не забыв про точку C, видим, что по формуле Пика площадь
треугольника ABC равна 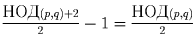 .
Поскольку
.
Поскольку 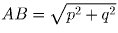 , высота треугольника ABC вычисляется
по формуле
, высота треугольника ABC вычисляется
по формуле
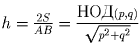 .
.