Задача 1:
Доказать, что сумма расстояний от произвольной точки внутри
треугольника до его вершин больше полупериметра.
Решение:
OA + OB > AB; OB + OC > BC; OA + OC > AC, значит
2(OA + OB + OC) > AB + BC + AC.
Задача 2:
Ученики ЛМШ-3001 посещают 14 клубов, причём в каждом клубе ровно 4
слушателя, и любые два клуба имеют ровно одного общего слушателя. Докажите,
что есть ученик, посещающий все клубы.
Решение:
Рассмотрим произвольный клуб. Его посещают четыре ученика. Так как эти
ученики должны посетить все остальные 13 клубов, то один из них (Вася)
посещает по крайней мере четыре других клуба (итого – 5). Обозначим их
буквами A, B, C, D, E. Обратим внимание, что именно Вася
является общим
слушателем каждой пары из этих клубов (а других общих слушателей по условию
нет). Теперь рассматриваем любой из остальных 9 клубов – X. Для каждого из
клубов A, B, C, D, E в клубе X должен быть ученик, который посещает этот
клуб. Но так как в X ровно 4 слушателя, то для каких-то двух из них эти
слушатели совпадут. Следовательно, этим самым совпадающим слушателем будет
Вася. Мы доказали, что Вася посещает все клубы.
Задача 3:
Верно ли, что среди любых 12 последовательных трёхзначных чисел не
более четырёх простых?
Решение:
Среди чисел есть шесть чётных чисел и два нечётных числа, делящихся на
три…
Задача 4:
В классе 33 ученика, всем им вместе 430 лет. Докажите, что в классе
найдутся 20 учеников, которым вместе не менее 260 лет.
Решение:
Возраст двадцати старших учеников не менее
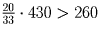
.
Задача 5:
Леня по одной достает и складывает в две стопки черные и красные
карточки. Класть карточку на другую карточку того же цвета запрещено.
Десятая и одиннадцатая карточки были красные, а двадцать пятая – черная.
Какого цвета была двадцать шестая?
Решение:
Состояния верха кучки чередуются: сначала одинаковые, потом разные,
потом снова одинаковые…После одиннадцатой карточки одинаковые,
значит после двадцать пятой – тоже одинаковые (чёрные). Значит
двадцать шестая карточка – красная.
Задача 6:
На доске написаны 6 чисел 1, 2, 3, 4, 5, 6. Разрешается к любым двум
прибавить по 1. Можно ли, проделав эту операцию несколько раз, сделать все
числа равными?
Решение:
Нет. Инвариант – чётность суммы (количества нечётных чисел).
Задача 7:
Никита написал на доске пять единиц, а потом вставил между ними
некоторое количество нулей. Он утверждает, что получилось число, которое
является квадратом некоторого целого числа. Прав ли Никита?
Решение:
Нет, потому что полученное число делится на три, но не делится на 9.
Задача 8:
Из шести спичек одинаковой длины
выложен шестиугольник ABCDEF, причем
противолежащие спички лежат параллельно. Доказать, что площади треугольников
ACE и BDF равны.


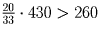 .
Задача 5:
Леня по одной достает и складывает в две стопки черные и красные
карточки. Класть карточку на другую карточку того же цвета запрещено.
Десятая и одиннадцатая карточки были красные, а двадцать пятая – черная.
Какого цвета была двадцать шестая?
Решение:
Состояния верха кучки чередуются: сначала одинаковые, потом разные,
потом снова одинаковые…После одиннадцатой карточки одинаковые,
значит после двадцать пятой – тоже одинаковые (чёрные). Значит
двадцать шестая карточка – красная.
.
Задача 5:
Леня по одной достает и складывает в две стопки черные и красные
карточки. Класть карточку на другую карточку того же цвета запрещено.
Десятая и одиннадцатая карточки были красные, а двадцать пятая – черная.
Какого цвета была двадцать шестая?
Решение:
Состояния верха кучки чередуются: сначала одинаковые, потом разные,
потом снова одинаковые…После одиннадцатой карточки одинаковые,
значит после двадцать пятой – тоже одинаковые (чёрные). Значит
двадцать шестая карточка – красная.