 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Разрезания | Убрать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2001 г, 7 класс. Разрезания |
|
|
б) квадрат 4 × 4 на 5 равных частей?
Решение: а)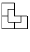
Задача 2: Семиклассник разрезал квадрат на прямоугольники периметра 7, а восьмиклассник – на прямоугольники периметра 8. Могло ли у восьмиклассника получиться больше прямоугольников? Решение: Да. Например, семиклассник может разрезать квадрат на прямоугольники 2.5 × 1, а восьмиклассник – на прямоугольники 0.5 × 3.5 Задача 3: Можно ли разрезать квадрат на 3 десятиугольника и 33-угольник? Решение: а) 3, 4, 5, 6, 7, 8, 9, 10.
б) Да. Например, строим внутри квадрата три не имеющие общих вершин десятиугольники так, чтобы по две вершины каждого лежали на одной из сторон квадрата причём одна из таких вершин совпадала с вершиной квадрата
в) Да
Задача 4: Можно ли разрезать квадрат на равносторонние треугольники? Решение: нет, так как не удаётся заполнить угол в квадрате.Задача 5: Для каких значений n можно разрезать а) квадрат на n меньших (не обязательно одинаковых) квадратов; б) правильный треугольник на n меньших (не обязательно одинаковых) правильных треугольников? Решение: а) n = 4 или n ≥ 6; б) n = 4 или n ≥ 6.
Задача 6: Разрежьте квадрат 7 × 7 на
а) квадраты 4 × 4, квадрат 3 × 3 и 4 равных прямоугольных треугольника;
б) один квадрат и 4 прямоугольных треугольника, равных треугольникам из (а);
в) Найдите размер квадрата в (б).
Задача 7: Даны 4 прямоугольных треугольника с катетами a, b и гипотенузой c. Докажите, что добавив к ним а) один квадрат со стороной c; б) два квадрата со сторонами a и b, можно будет составить квадрат со стороной a + b.
Задача 8: [Теорема Пифагора] Докажите, что a² + b² = c².
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Разрезания | Убрать решения |