Задача 1:

Ваш друг задумал многочлен F(x) с натуральными коэффициентами. Вам разрешается просить его вычислить F(m₁) для какого-то натурального числа m₁ и, получив ответ, попросить его вычислить F(m₂) для какого-нибудь другого натурального числа m₂. Можете Вы таким образом восстановить многочлен F(x)?

Задача 2:

a, b и c – попарно взаимно простые натуральные числа. Докажите, что существует бесконечно много троек (x,y,z) различных натуральных чисел x, y, z таких, что x^a + y^b = z^c.

Задача 3:

I – центр вписанной окружности треугольника ABC, T – центр описанной окружности треугольника BIC. Докажите что точка T лежит на биссектрисе угла A.

Задача 4:

(n + 1)n/2 камней разложены в несколько кучек. За один ход из каждой кучки берут камень и помещают все собранные камни в новую кучку. Докажите, что через несколько ходов будет n кучек состоящих из 1, 2,…...,n камней, соответственно.

Задача 5:

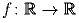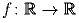Существует ли такая функция , что f(f(x)) = e^x?