 |
 |
|
| Задачная база >> Международные соревнования >> Азиатско-Тихоокеанская МО >> 1991 | Убрать решения |
|
|
| Международные соревнования. Азиатско-Тихоокеанская МО. 1991 |
|
|
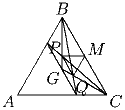
G – центр тяжести треугольника ABC, M – середина стороны BC. Точки X и Y выбрали на сторонах AB и AC так, что XY параллельно BC и точки X,Y,G лежат на одной прямой. XC и GB пересекаются в точке Q, а YB и GC – в точке P. Докажите, что треугольники MPQ и ABC подобны.
На плоскости отмечено 997 точек. Каждые две из отмеченных точек соединили отрезками и середины каждого отрезка покрасили в красный цвет. Докажите, что количество красных точек на плоскости не менее 1991. Можете ли вы привести пример, когда их будет ровно 1991?
Задача 3:a1,a2, … ,an,b1,b2, … ,bn – положительные вещественные числа такие, что a1 + a2 + … + an = b1 + b2 + … + bn. Докажите, что
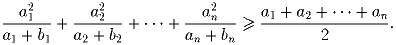
n школьников сидят вокруг учителя, который раздает леденцы. Учитель выбрал первого попавшегося ребенка и дал ему леденец, следующий леденец он дал ребенку сидящему через одного от первого по часовой стрелке, затем он пропустил еще двух школьников, и дал леденец следующему ребенку, затем он пропустил трех и так далее…Найдите все значения n при которых рано или поздно каждый ребенок получит хотябы по одному леденцу.
Задача 5:Даны две касающиеся окружности и точка P на их общей касательной, проведенной в точке касания окружностей. Пользуясь только циркулем и линейкой постройте окружность проходящую через точку P и касающуюся данных.
| Задачная база >> Международные соревнования >> Азиатско-Тихоокеанская МО >> 1991 | Убрать решения |