Задача 1:

ABCD – четырехугольник, все стороны которого равны и  ∠ ABC = 60°. l – прямая проходящая через D и не пересекающаяся четырехугольник ни в какой другой точке. E и F – точки пересечения l с прямыми AB и BC соответственно, M – точка пересечения CE и AF. Докажите, что AC² = CM • CE.

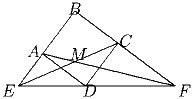
Задача 2:

Найдите общее число различных целых значений, принимаемых функцией f(x) = [x] + [2x] + [5x/3] + [3x] + [4x] на отрезке [\,0,\,100\,].

Задача 3:

Даны два ненулевых многочлена с вещественными коэффициентами f(x) и g(x) такие, что g(x) = (x + r)f(x), для некоторого вещественного r. Пусть a =  max (|a₀|,|a₁|, … ,|a_n|), c =  max (|c₀|,|c₁|, … ,|c_n + 1|), где a_i – коэффициенты многочлена f, а c_i – коэффициенты g. Докажите, что если степень многочлена f равна n, то a/c ≤ n + 1.

Задача 4:

Найдите все натуральные n, при которых уравнение xⁿ + (2 + x)ⁿ + (2 – x)ⁿ = 0 имеет целое решение.

Задача 5:

P₁,P₂, … ,P₁₉₉₃ = P₀ – различные точки плоскости такие, что

• [(1)] для всех i обе координаты P_i – целые числа;
• [(2)] на каждом из отрезков P_iP_i + 1 нет точек с целыми координатами, отличных от P_i и P_i + 1.

Докажите, что на одном из отрезков P_iP_i + 1 найдется точка Q с координатами (q_x,q_y) такая, что числа 2q_x и 2q_y – нечетные целые.