Задача 1: Найдите все последовательности вещественных чисел
a1,a2, … ,a1995 удовлетворяющие неравенствам:
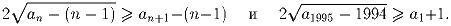
Задача 2: a1,a2, … ,an – последовательность целых чисел из отрезка
[2,1995] такая, что
- [(1)] любые два члена последовательности взаимно просты;
- [(2)] каждый член последовательности является либо простым числом,
либо произведением различных простых чисел.
Найдите наименьшее n, такое, что в последовательности a
i наверняка
будет по крайней мере одно простое число.
Задача 3: PQRS – описанный четырехугольник, стороны которого PQ и RS не
параллельны. Рассмотрим семейство окружностей проходящих через точки P и
Q и семейство окружностей, проходящих через точки R и S. Определите
геометрическое место точек касания окружностей этих двух семейств.
Задача 4: C – окружность радиуса R с центром в точке O, S –
некоторая точка внутри нее. AA′ и BB′ – две перпендикулярные хорды
проходящие через S. Рассмотрим прямоугольники SAMB,SBN′A′,SA′M′B′ и
SB′NA. Найдите геометрическое место точек M,N′,M′,N, когда точка A
описывает всю окружность C.
Задача 5: Найдите такое минимальное k, что существует отображение
f множества целых чисел 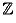 в множество 1,2, … ,k со
свойством f(x) ≠ f(y) при |x – y| ∈ 5,7,12.
в множество 1,2, … ,k со
свойством f(x) ≠ f(y) при |x – y| ∈ 5,7,12.


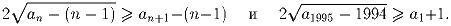
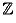 в множество 1,2, … ,k со
свойством f(x) ≠ f(y) при |x – y| ∈ 5,7,12.
в множество 1,2, … ,k со
свойством f(x) ≠ f(y) при |x – y| ∈ 5,7,12.