Задача 1: Пусть n – натуральное число. Докажите, что если a и b – большие 1
натуральные числа такие, что 2n – 1 = ab, то ab – (a – b) – 1 есть число вида
k • 22m, где k – некоторое нечётное число,
а m – некоторое натуральное число.
Задача 2: Докажите, что если у пятиугольника все внутренние углы равны,
а все стороны имеют рациональную длину, то пятиугольник правильный.
Задача 3: a, b и c – положительные вещественные числа такие, что
a + b + c ≥ abc. Докажите, что 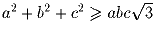 .
.
Задача 4: Куб размера 3 × 3 × 3 разбит на 27 кубических ячеек со стороной 1.
Одна из ячеек пуста, в остальных лежат кубики, в некотором порядке
пронумерованные числами 1, 2,…,26. Разрешённый ход состоит в
передвижении кубика в соседнюю пустую ячейку (две ячейки считаются соседними,
если они имеют общую грань). Существует ли такая
конечная последовательность разрешённых ходов, при которой для любого
k = 1, … 13 кубики k и 27 – k поменяются местами?


 .
.