 |
 |
|
| Задачная база >> Международные соревнования >> Международная МО >> 2 олимпиада | Убрать решения |
|
|
| Международные соревнования. Международная МО. 2 олимпиада |
|
|
Найдит все трехзначные числа N которые делятся на 11 и N/11 равно сумме квадратов цифр N.
Задача 2:При каких x выполняется неравенство
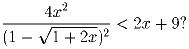
Гипотенузу BC треугольника ABC поделили на n равных частей,
где n – нечетное число. Цетральная часть гипотенузы видна из
вершины A под углом α . Докажите, что
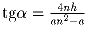 , где h – длина высоты, опущенной
на BC, a – длина BC.
, где h – длина высоты, опущенной
на BC, a – длина BC.
Постройте треугольник ABC по высотам, опущенным из A и B и медиане, проведенной из A.
Задача 5:Точка X лежит на диагонали AC, а точка Y – на диагонали B′D′ куба ABCDA′B′C′D′.
a) найдите геометрическое место середин отрезков XY;
b) найдите геометрическое место точек Z таких, что ZY = 2XZ (Z ∈ XY).
Задача 6:В конус объема V1 вписана сфера, вокруг которой описан цилиндр объема V2. Докажите, что V1 ≠ V2 и найдите наименьшее значение V1/V2.
| Задачная база >> Международные соревнования >> Международная МО >> 2 олимпиада | Убрать решения |