Задача 1:
[Чехо-Словакия]
Площадь плоского выпуклого четырехугольника
равна 32 см², а сумма длин двух противоположных сторон и одной
диагонали равна 16 см. Указать все значения, которые может
принимать длина другой диагонали.
Задача 2:
[Финляндия]
Пусть P(x) = x² – 2, P
k(x) = P
1(P
k – 1(x))
(k = 2,3, … ). Доказать, что для любого натурального n все
корни уравнения P
n(x) = x вещественны и различны.
Задача 3:
[Нидерланды]
Прямоугольная коробка может быть полностью
наполнена единичными кубами (ребра кубов параллельны ребрам
коробки). Если же заполнить коробку кубами объема 2 с ребрами,
параллельными ребрам коробки, то максимальное число таких кубов
заполнит лишь 40 объема коробки. Указать внутренние размеры всех
коробок, для которых это имеет место (
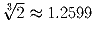
).
Задача 4:
[США] Найти наибольшее значение, которое может принять
произведение нескольких натуральных чисел, сумма которых равна
1976.
Задача 5:
[Нидерланды]
В системе p уравнений с q = 2p неизвестными
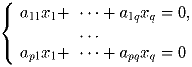
коэффициенты a
ij ∈ – 1,0,1. Доказать, что существует
решение (x
1,x
2, … ,x
q) этой системы такое, что все x
j
(1 ≤ j ≤ q) – целые числа, по модулю меньшие q и при
этом не все равны нулю.
Задача 6:
[Великобритания]
Последовательность u
n определяется
следующим образом:
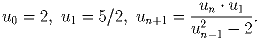
Доказать, что при n ≥ 1
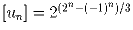
.


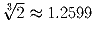 ).
Задача 4:
[США] Найти наибольшее значение, которое может принять
произведение нескольких натуральных чисел, сумма которых равна
1976.
Задача 5:
[Нидерланды]
В системе p уравнений с q = 2p неизвестными
).
Задача 4:
[США] Найти наибольшее значение, которое может принять
произведение нескольких натуральных чисел, сумма которых равна
1976.
Задача 5:
[Нидерланды]
В системе p уравнений с q = 2p неизвестными
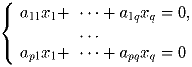
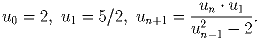
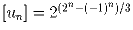 .
.