 |
 |
|
| Задачная база >> Международные соревнования >> Международная МО >> 23 олимпиада | Убрать решения |
|
|
| Международные соревнования. Международная МО. 23 олимпиада |
|
|
Дан неравнобедренный треугольник A1A2A3. Пусть ai – его сторона, лежащая против вершины Ai (i = 1,2,3), Mi – середина стороны ai, Ti – точка касания стороны с окружностью, вписанной в данный треугольник, и Si – точка, симметричная Ti относительно биссектрисы угла Ai треугольника. Докажите, что прямые M1S1, M2S2, M3S3 имеют общую точку.
Задача 2: [СССР,А.Гришков] Рассматриваются последовательности xn положительных чисел, удовлетворяющих условию 1 = x0 ≥ x1 ≥ x2 ≥ … ≥ xn ≥ …а) Докажите, что для любой такой последовательности xn существует n, при котором
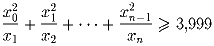
б) Найдите такую последовательность xn, удовлетворяющую указанному условию, для которой при любом n
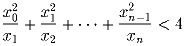
а) при любых m и n f(m + n) – f(m) – f(n) принимает значения 0 или 1,
б) f(2) = 0,
в) f(3) > 0,
г) f(9999) = 3333.
Найти f(1982).
Задача 4:На диагоналях AC и CE правильного шестиугольника ABCDEF взяты
точки M и N такие, что 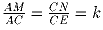 . Известно,
что точки B, M и N лежат на одной окружности. Найдите k.
. Известно,
что точки B, M и N лежат на одной окружности. Найдите k.
Дано уравнение x³ – 3xy² + y³ = n. Докажите, что
а) если натуральное n таково, что данное уравнение имеет целочисленное решение, то оно имеет по меньшей мере три целочисленных решения;
б) при n = 2891 это уравнение не имеет целочисленных решений.
Задача 6:Дан квадрат K со стороной 100. Пусть L – несамопересекающаяся незамкнутая ломаная, лежащая в K, такая, что для любой точки P границы квадрата K найдется точка ломаной L, расстояние которой от P не больше 1/2. Докажите, что на ломаной найдутся две точки X и Y, расстояние между которыми не более 1, такие, что длина части ломаной, заключенной между ними, не меньше 198.
| Задачная база >> Международные соревнования >> Международная МО >> 23 олимпиада | Убрать решения |