 |
 |
|
| Задачная база >> Международные соревнования >> Международная МО >> 30 олимпиада | Убрать решения |
|
|
| Международные соревнования. Международная МО. 30 олимпиада |
|
|
а) каждое из множеств Ai имеет 17 элементов;
б) S1 = S2 = … S117, где Si – сумма всех чисел множества Ai.
Задача 2: [Австралия] Биссектрисы углов A, B, C остроугольного треугольника ABC пересекают описанную около него окружность в точках A1, B1, C1 соответственно. Прямая AAi пересекает биссектрисы внешних углов при вершинах B и C треугольника ABC в точке A0. Точки B0 и C0 определяются аналогично.Докажите, что
а) 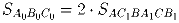
б) 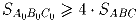
а) никакие три точки из S не лежат на одной прямой;
б) для любой точки P ∈ S существуют не менее k различных точек из S, равноудаленных от P.
Докажите, что
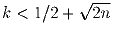
Докажите, что
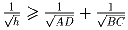
| Задачная база >> Международные соревнования >> Международная МО >> 30 олимпиада | Убрать решения |