Задача 1: [Индия] Хорды AB и CD пересекаются в точке E внутри данной окружности. Пусть M – внутренняя точка отрезка BE. Касательная в точке E к окружности, проходящей через точки D, E и M, пересекает прямые BC и AC в точках F и G соответственно. Пусть AM/AB = t. Найдите EG/EF как функцию от t.

Задача 2: [Чехо-Словакия] На окружности дано множество E из 2n – 1 различных точек (n ≥ 3), из которых k точек покрашены в черный цвет, а остальные – в белый. Раскраска точек называется хорошей, если существуют две черные точки, строго между которыми на одной из дуг окружности содержится ровно n точек из множества E. Найдите наименьшее значение k, для которого каждая раскраска точек множества E является хорошей.

Задача 3: [Румыния] Найдите все целые числа n > 1 такие, что (2ⁿ + 1)/n² является целым числом.

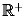Задача 4: [Турция] Пусть  – множество всех положительных рациональных чисел. Приведите пример функции 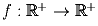такой, что f(x • f(y)) = f(x)/y для всех .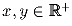

Задача 5: [ФРГ] Дано натуральное число n₀ > 1. Игроки A и B выбирают по очереди натуральные числа n₁,n₂, …  по следующему индуктивному правилу. Игрок A, зная число n_2k, может выбрать любое число n_2k + 1 такое, что

Затем игрок B выбирает любое число n_2k + 2 такое, что n_2k + 1/n_2k + 2 является положительной натуральной степенью простого числа. Игрок A побеждает тогда, когда выберет число 1990, а B – когда выберет 1.

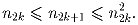
Найдите все значения n₀, для которых

а) A имеет выигрышную стратегию;

б) B имеет выигрышную стратегию;

в) ни у A, ни у B нет выигрышных стратегий.

Задача 6: [Нидерланды] Докажите, что существует выпуклый многоугольник с 1990 сторонами такой, что

а) все его углы равны;

б) длины сторон многоугольника равны числам 1², 2², …, 1989², 1990² в некотором порядке.