Задача 1: Окружности  Γ ₁ и  Γ ₂ пересекаются в точках M и N. Прямая l – общая касательная к  Γ ₁ и  Γ ₂ такая, что M расположена к l ближе, чем N. Прямая l касается  Γ ₁ в точке A, а  Γ ₂ – в точке B. Прямая, проходящая через M параллельно l, пересекает вторично окружность  Γ ₁ в точке C, а окружность  Γ ₂ – в точке D. Прямые CA и DB пересекаются в точке E, прямые AN и CD – в точке P, прямые BN и CD – в точке Q. Докажите, что EP = EQ.

Решение:  ∠ EBA =  ∠ BDM (так как CD\|AB)  =  ∠ ABM (т.к. AB – касательная в точке B), значит AB – биссектриса  ∠ EBM. Аналогично BA – биссектриса  ∠ EAM. Поэтому точка E – симметрична точке M относительно AB, откуда следует, что EM перпендикулярно AB, а значит и CD.

Осталось показать, что MP = MQ. Пусть прямые NM и AB перескаются в точке X. XA – касательная, поэтому XA² = XM • XN. Аналогично, XB² = XM • XN. Таким образом, XA = XB. Но AB\|PQ, поэтому MP = MQ.

Задача 2: Положительные числа a, b, c таковы, что abc = 1. Докажите, что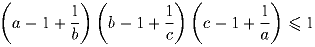

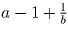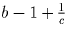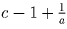Решение: Пусть числа , , положительны. Заметим, что

Отсюда следует, что

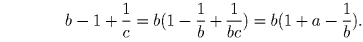
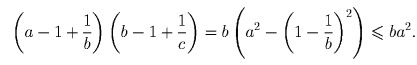
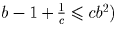Аналогично и 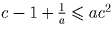. Перемножив эти три неравенства, получаем, что

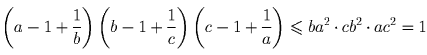
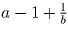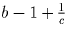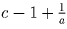Если же хотя бы одно из чисел , и отрицательно, то два других положительны. Например, если 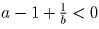, то a < 1, поэтому 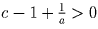, а b > 1, поэтому .

Задача 3:

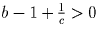Дано натуральное число n > 2. Сначала на горизонтальной прямой сидят n блох, не все в одной точке. Для положительного действительного числа  λ  определим прыжок следующим образом: выбираются две блохи, сидящие в произвольных точках A и B, причём A левее B, и блоха, сидящая в A, прыгает в точку C, расположенную на данной прямой справа от B, такую, что 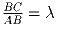. Определите все значения  λ  такие, что для любой точки M на этой прямой и для любого начального расположения n блох существует конечная последовательность прыжков, после которой все блохи окажутся справа от точки M.

Решение: Ответ: .

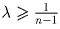Предположим, что 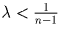, тогда 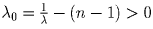. Пусть X – сумма расстояний блох от самой правой блохи. Если в точке B сидит не самая правая бложа, то X уменьшается. Пусть в точке B сидит самая правая блоха. Тогда после прыжка самая правая блоха будет на |BC| правее, чем раньше, а X уменьшится по крайней мере на 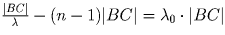. X не может стать меньше 0. Поэтому общее расстояние, на которое сдвинулась самая правая точка, не превосходит 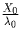, где X₀ – начальное значение X.

Пусть теперь 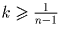, тогда 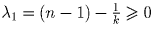. В качестве точки A будем брать точку, в которой сидит самая левая блоха, а в качестве точки B – точку в которой сидит самая правая блоха. После прыжка самая правая блоха будет на |BC| правее, а X увеличится на 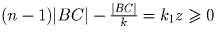. Таким образом, X никогда не уменьшается. Но 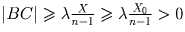, а значит самая правая блоха может оказаться сколь угодно далеко справа. Остальным блохам теперь остаётся только перепрыгнуть через неё.

Задача 4:

У фокусника 100 карточек, занумерованных числами от 1 до 100. Он раскладывает все карточки в три ящика: красный, белый и синий так, чтобы в каждом ящике лежала хотя бы одна карточка. Один из зрителей выбирает два из трёх ящиков, вынимает из них по одной карточке и объявляет сумму номеров вынутых карточек. Зная эту сумму, фокусник определяет тот ящик, из которого карточка не вынималась. Сколькими различными способами можно разложить карточки по ящикам так, чтобы этот фокус всегда удавался? (Способы, при которых хотя бы одна карточка попадает в разные ящики, считаются различными.)

Решение: Ответ: 12. Пометить ящики числами 0, 1, 2 (6 возможностей), и класть карточку n в коробку, на которой написан остаток n от деления на 3. Или поместить 1 и 100 в разные ящики, а 2 – 99 – в третий ящик (ещё 6 возможностей).

Пусть H_n – утверждение, что для карточек, пронумерованных от 1 до n единственные решения – разложить по остаткам от деления на 3, и поместить карточки 1 и n в разные ящики, а карточки от 2-й до (n – 1)-й – в третий ящик. Легко проверить, что это действительно решения. H_n утверждает, что других решений нет. H₃ очевидно истинно (хотя оба случая совпадают). Используем индукцию по n. Предположим, что H_n истинно, и докажем, что H_n + 1 истинно.

Предположим, что карточка n + 1 единственна в своём ящике. Если карточка 1 не единственна в своём ящике, то пусть N – сумма максимальных карточек в ящиках (кроме n + 1). Поскольку n + 2 ≤ N ≤ n + (n – 1) = 2n – 1, мы можем достичь такой же суммы N в другой паре ящиков ((n + 1) + (N – n – 1)). противоречие. Значит карточка 1 единственна в своём ящике, и мы получили одно из решений, описанных в H_n + 1.

Если n + 1 не единственна в своём ящике, то, если мы уберём её, то должны получить решение для n. Нетрудно проверить, что это не может быть (n,1,2..n – 1)-решение, поэтому карточки 1..n распределены в соответствии с их остатками при делении на 3. То, что карточка n + 1 должна лежать в ящике с соответствующим остатком, очевидно.

Задача 5: Существует ли натуральное число n такое, что n имеет ровно 2000 различных простых делителей, и 2ⁿ + 1 делится на n.

Решение:

Ответ: да.

Заметим, что для нечётных b 2^ab + 1 = (2^a + 1)(2^a(b – 1) – 2^a(b – 2) +  …  + 1), поэтому 2^a + 1 – делитель 2^ab + 1. Поэтому достаточно найти такое m, что

1. у m мало различных простых делителей;
2. у 2^m + 1 много различных простых делителей;
3. 2^m + 1 делится на m.

Тогда мы сможем взять в качестве k произведение достаточного количества различных простых делителей 2^m + 1, на которые не делится m так, чтобы у km было ровно 2000 делителей. При этом km будет делителем 2^m + 1, а значит и 2^km + 1.

Возьмём m = 3^h. Надо проверить (1) делится ли a_h = 2^m + 1 на m = 3^h и (2) есть ли у него много простых делителей при достаточно больших h.

Заметим, что a_h + 1 = a_h(2^2m – 2^m + 1), где m = 3^h. Но 2^m = (a^h – 1), поэтому 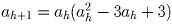. Учитывая, что a₁ = 9, с помощью несложной индукции получаем, что a_h делится на 3^h + 1, а значит и на m.

Остаётся убедиться, что мы сможем найти a_h с достаточно большим количеством простых делителей. Пусть a_h = mb_h. Тогда 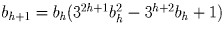. Учитывая, что в последнем выражении множители взаимно просты, а второй множитель больше единицы, нетрудно видеть, что у b_h + 1 есть простой делитель больший трёх, не являющийся делителем b_h. Но это означает, что у b_h при достаточно больших h будет достаточно много различных простых делителей больших трёх.

Мы показали, что взяв m из первого параграфа равным, скажем, 3²ººº, пролучим, что

1. у m есть только один простой делитель;
2. у 2^m + 1 = 3²ºº¹b²ººº по крайней мере 1999 различных простых делителей не равных 3.
3. 2^m + 1 делится на m.

Взяв k равным произведению 1999 различных простых делителей b²ººº, получим, что n = km – число ровно с 2000 различными простыми делителями, которое делит 2ⁿ + 1.

Задача 6: Пусть AH₁, BH₂, CH₃ – высоты остроугольного треугольника ABC. Окружность, вписанная в треугольник ABC, касается сторон BC, CA, AB в точках T₁, T₂, T₃ соответственно. Прямые l₁, l₂, l₃ являются образами прямых H₂H₃, H₃H₁, H₁H₂ при симметрии относительно прямых T₂T₃, T₃T₁, T₁T₂ соответственно. Докажите, что прямые l₁, l₂, l₃ образуют треугольник с вершинами на окружности, вписанной в треугольник ABC.

Решение:

Пусть O – центр вписанной окружности, а X – точка пересечения прямой проходящей через точку T₂ параллельно AB и прямой BO. Мы покажем, что точка X симметрична точке H₂ относительно прямой T₂T₃. Пусть AC пересекается с с BO в точке B₂. A₂H₂ ⊥ T₂B₂, поэтому  ∆ BH₂B₂ ∽  ∆ OT₂B₂. Значит 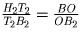. Но OA₃ – биссектриса треугольника BCB₂, поэтому .

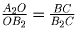Возьмём на прямой BO точку B′₂ так, что T₂B₂ = T₂B′₂ (B′₂ не совпадает с B₂, если T₂B₂ не перпендикулярно этой прямой). Тогда  ∠ T₂B′₂X =  ∠ CBB₂. Кроме того, поскольку T₂X\|BA,  ∠ T₂XB′₂ =  ∠ CBB₂. Таким образом,  ∆ T₂XB′₂ ∽  ∆ CBB₂. Значит 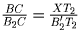(т.к. B′₂T₂ = B₂T₂).

Мы показали, что 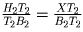, а значит H₂T₂ = XT₂. T₂X\|AB, поэтому  ∠ BAC =  ∠ AT₂X =  ∠ T₂H₂X = 2 ∠ T₂XH₂ (равнобедр.). Так что  ∠ T₂XH₂ = ½ ∠ BAC =  ∠ BAO. H₂X\|BA, значит и H₂X\|OA. Но OA ⊥ T₂T₃, значит и H₂X ⊥ T₂T₃. Значит X действительно симметрично H₂ относительно T₂T₃.

Теперь заметим, что  ∠ H₃H₂A₁ = 90 –  ∠ H₃H₂B = 90 – H₃CB =  ∠ ABC. Значит прямая симметричная H₂H₃ относительно T₂T₃ проходит через точку X, образуя  ∠ ABC с T₂X, а значит параллельна BC.

Пусть M₁, M₂, M₃ – точки симметричные точкам T₁, T₂ и T₃ относительно прямых AO, BO и CO соответственно.  ∠ M₂XT₂ = 2 ∠ OXT₂ = 2 ∠ ABO (поскольку AB\|T₂X)  =  ∠ ABC. Поэтому M₂X\|BC, то есть M₂ лежит на прямой, симметричной H₂H₃ относительно T₂T₃. Аналогично получаем, что на этой прямой лежит и M₃.

Точно так же прямая M₁M₃ симметрична прямой H₁H₃ относительно T₁T₃, а прямая M₁M₂ – прямой T₁T₂ относительно T₁T₂. Это означает, что треугольник образованный пересечением l₁, l₂ и l₃ – это и есть M₁M₂M₃.