Задача 1: На сторонах AB, BC и CA треугольника ABC взяты точки C′, A′ и B′ соответственно. Докажите, что площадь треугольника A′B′C′ равна

где R — радиус описанной окружности треугольника ABC.

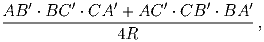
(Фольклор)

Задача 2: Вычислить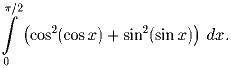

(М.Н.~Вялый, А.В.~Спивак)

Задача 3: Учитель написал на доске три функции: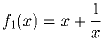 , f₂(x) = x², f₃(x) = (x – 1)² и предложил ученикам с помощью операций сложения, умножения, вычитания, операции умножения на произвольное число и операции сложения с произвольным числом получить функцию 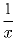. Выполните это задание и докажите, что при этом должны быть использованы все три функции.

(М.~Евдокимов)

Задача 4: Можно ли разбить правильный тетраэдр с ребром 1 на правильные тетраэдры и октаэдры, длины ребер каждого из которых меньше 1/100?

(В.В.~Произволов)

Задача 5: Положительные числа a, b и c таковы, что abc = 1. Докажите, что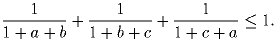

(Г.А.~Гальперин)

Задача 6: На плоскости дано конечное число полос, сумма ширин которых равна 100, и круг радиуса 1. Доказать, что каждую из полос можно параллельно перенести так, чтобы все они покрывали круг.

(М.В.~Смуров)