 |
 |
|
| Задачная база >> Московские соревнования >> Городская олимпиада >> 1997 >> Городской тур >> 6 класс | Убрать решения |
|
|
| LX Московская математическая олимпиада. Городской тур. 6 класс |
|
|
314159[-2mm] +[-2mm] 291828585787
(В.~Замков)
Задача 2: В папирусе Ринда (Древний Египет) среди прочих сведений содержатся разложения дробей в сумму дробей с числителем 1, например,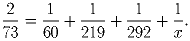
(А.В.~Спивак)
Задача 3: В корзине лежат 30 грибов — рыжиков и груздей. Известно, что среди любых 12 грибов имеется хотя бы один рыжик, а среди любых 20 грибов — хотя бы один груздь. Сколько рыжиков и сколько груздей в корзине?
(А.И.~Галочкин)
Задача 4: Разрежьте изображенную доску на 4 одинаковые части, чтобы каждая из них содержала 3 заштрихованные клетки.
(Фольклор)
Задача 5: Придумайте раскраску граней кубика, чтобы в трех различных положениях он выглядел, как показано на рисунке. (Укажите, как раскрасить невидимые грани или нарисуйте развертку.)
(Фольклор)
Задача 6: Семья ночью подошла к мосту. Папа может перейти его за 1 минуту, мама — за 2, малыш — за 5, а бабушка — за 10 минут. У них есть один фонарик. Двигаться по мосту без фонарика нельзя. Мост выдерживает только двоих. Если переходят двое, то более быстрый идет со скоростью более медлительного. Как им перейти мост за 17 минут?
(Из электронной конференции rec.puzzles)
| Задачная база >> Московские соревнования >> Городская олимпиада >> 1997 >> Городской тур >> 6 класс | Убрать решения |