Задача 1:
Существуют ли два последовательных натуральных числа,
сумма цифр каждого из которых делится на 1997?
Задача 2:
Пусть f(x) — функция и для любых a и b выполняется
равенство f(a + b) + f(a – b) = 2f(a) + 2f(b). Является ли эта
функция четной?
Задача 3:
Докажите неравенство (1 + x)
1997 ≥ 1 + 1997x при x ≥ 0.
Задача 4:
Найдите наименьшее значение выражения
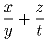
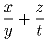при 1 ≤ x ≤ y ≤ z ≤ t ≤ 100.
Задача 5:
Около правильного тетраэдра ABCD описана сфера. На его
гранях построены во внешнюю сторону как на основаниях правильные
пирамиды ABCD′, ABDC′, ACDB′, BCDA′, вершины которых
лежат на этой сфере. Найти угол между плоскостями ABC′ и
ACD′.
