Задача 1: В параллелограмме ABCD точка E — середина стороны AD, F — основание перпендикуляра, опущенного из вершины B на прямую CE. Доказать, что AF = AB.

Задача 2: Фигура M в пространстве представляет собой пересечение единичного куба 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1 с полупространством ax + by + cz ≤ d (a, b и c — положительные числа). Докажите, что объем M равен

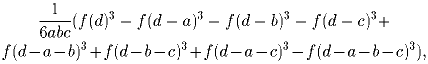
где f(x) =  max (x,0).

Задача 3: В каждой клетке шахматной доски стоит знак  +  или  – . Разрешается одновременно заменять все знаки, стоящие в одной строке или в одном столбце на противоположные. Докажите, что с помощью многократного применения этой операции можно сделать все знаки плюсами тогда и только тогда, когда в любом квадрате 2 × 2 стоит четное число плюсов.

Задача 4: Фанерный прямоугольник расчерчен отрезками на прямоугольники. Докажите, что по этим отрезкам его можно распилить ножовкой (пилить можно только от края, поворачивать нельзя, отпиленные куски разнимаются).

Задача 5: Для каждого натурального числа n обозначим через A_n множество натуральных чисел, больших единицы, дающих при делении на n остаток единица. Назовем число из A_n неприводимым, если оно не представимо в виде произведения двух меньших чисел из A_n. Докажите, что для любого n > 2 найдется число в A_n, представимое в виде произведения неприводимых в A_n чисел различными способами.

Задача 6: Задано натуральное число n > 3. Верно ли, что среди всех n-угольников (не только выпуклых) наибольшую сумму синусов внутренних углов имеет правильный?