 |
 |
|
| Задачная база >> Московские соревнования >> Городская олимпиада >> 2001 >> Городской тур >> 10 класс | Убрать решения |
|
|
| 64 Московская математическая олимпиада. Городской тур. 10 класс |
|
|
Существуют ли три квадратных трёхчлена, такие что каждый из них имеет корень, а сумма любых двух трёхчленов не имеет корней? (А. Канель)
Решение: =1Ответ: да, существуют. Например, таковыми являются многочлены x², (x – 1)² и (x – 2)². Сумма любых двух из них больше нуля при любом x.
Задача 2:
Можно ли расставить охрану вокруг точечного объекта так, чтобы ни к объекту, ни к часовым нельзя было незаметно подкрасться? (Каждый часовой стоит неподвижно и видит на 100 м строго вперёд.)
(В. Клепцын)
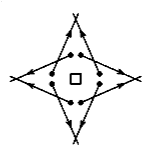
Решение: =2Ответ: да, можно. На рисунке показан пример расположения восьми часовых, удовлетворяющий условию. Кружочками обозначены часовые, каждая из стрелок указывает направление, в котором смотрит часовой.
Задача 3:
Приведите пример многочлена P(x) степени 2001, для которого выполняется тождество
P(x) + P(1 – x) = 1.
(В. Сендеров)
Решение: =3Например, P(x) = 2²ººº(x – ½)²ºº¹ + ½. График этой функции (рис.) получается из графика нечётной функции y = x²001 сдвигом вправо на ½, растяжением и сдвигом вверх на ½ и поэтому имеет центр симметрии M(½;½). Теперь легко понять, что P(1 – x) = 1 – P(x).

Задача 4:
В остроугольном треугольнике ABC проведены высоты AHA, BHB и CHC. Докажите, что треугольник с вершинами в точках пересечения высот треугольников AHBHC, BHAHC, CHAHB равен треугольнику HAHBHC.
(А. Акопян)
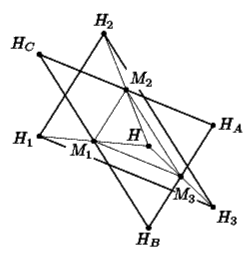
Решение: =4Пусть H1, H2, H3 – ортоцентры (точки пересечения высот) треугольников AHBHC, BHAHC, CHAHB соответственно, H – ортоцентр треугольника ABC, M1, M2, M3 – середины HBHC, HCHA и HAHB. Покажем, что точка Hi симметрична точке H относительно Mi (i = 1,2,3). Рассмотрим, например, точку H2. Поскольку HCH2\|BC и AH\|BC, отрезки HCH2 и HHA параллельны (см. рис.).
Так как M1M2 – общая средняя линия треугольников HAHBHC, и H1H2H, отрезки HAHB и H1H2 равны. Аналогично доказываются равенства HBHC = H2H3 и HAHC = H1H3. Следовательно, треугольники H1H2H3 и HAHBHC равны.
Получаем конфигурацию, показанную на рисунке.
Так как M1M2 – общая средняя линия треугольников HAHBHC и H1H2H отрезки HAHB и H1H2 равны. Аналогично доказываются равенства HBHC = H2H3 и HAHC = H1H3. Следовательно, треугольники H1H2H3 и HAHBHC равны.
На двух клетках шахматной доски стоят чёрная и белая фишки. За один ход можно передвинуть любую из них на соседнюю по вертикали или горизонтали клетку (две фишки не могут стоять на одной клетке). Могут ли в результате таких ходов встретиться все возможные варианты расположения этих двух фишек, причём ровно по одному разу?
(А. Шаповалов)
Решение: =5Ответ: не могут. Назовём расположение фишек одноцветным, если фишки стоят на клетках одного цвета, разноцветным – если на клетках разного цвета. Заметим, что при перемещениях фишек одноцветные и разноцветные расположения чередуются, значит, их должно быть поровну. Однако общее количество разноцветных расположений равно 2 • 32², а одноцветных – 2 • 32 × 31, поскольку две фишки не могут стоять на одной клетке. Значит, все возможные расположения встретиться не могут.
Задача 6:В игре «Десант» две армии захватывают страну. Они ходят по очереди, каждым ходом занимая один из свободных городов. Первый свой город армия захватывает с воздуха, а каждым следующим ходом она может захватить любой город, соединённый дорогой с каким-нибудь уже занятым этой армией городом. Если таких городов нет, армия прекращает боевые действия (при этом, возможно, другая армия свои действия продолжает). Найдётся ли такая схема городов и дорог, что армия, ходящая второй, сможет захватить более половины всех городов, как бы ни действовала первая армия? (Число городов конечно, каждая дорога соединяет ровно два города.)
(П. Грозман, А. Шаповалов, Д. Шаповалов)
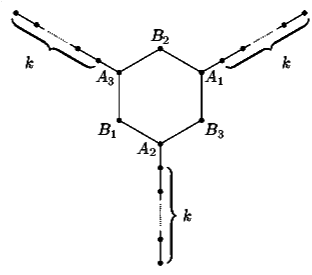
Решение: =6Ответ: да, найдётся. Рассмотрим страну, карта которой изображена на рисунке (точки – города, отрезки – дороги).
Покажем, что второй армии всегда удастся захватить хотя бы две точки Ai. Действительно, если первая армия первым ходом занимает точку на «ветке» из k точек, вторая армия должна занять соответствующую этой «ветке» точку Ai; если первая занимает Ai, то вторая – Bi; если первая выбирает точку Bi, то вторая – одну из точек Aj, соединенную отрезком с Bi. Дальнейшие действия очевидны.
Так как после прекращения боевых действий вторая армия занимает хотя бы
две точки Ai, первая занимает не более k + 3 точек. Поэтому доля городов,
захваченных второй армией, не менее 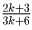 . Уже при k = 1 это
число больше ½. Заметим, что в условии задачи вместо
½ можно взять любое
число a < ⅔: при достаточно больших k
число
. Уже при k = 1 это
число больше ½. Заметим, что в условии задачи вместо
½ можно взять любое
число a < ⅔: при достаточно больших k
число 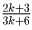 будет больше a.
будет больше a.
| Задачная база >> Московские соревнования >> Городская олимпиада >> 2001 >> Городской тур >> 10 класс | Убрать решения |