 |
 |
|
| Задачная база >> Московские соревнования >> Городская олимпиада >> 2001 >> Городской тур >> 8 класс | Убрать решения |
|
|
| 64 Московская математическая олимпиада. Городской тур. 8 класс |
|
|
На клетчатой бумаге нарисован прямоугольник шириной 200 и высотой 100 клеток. Его закрашивают по клеткам, начав с левой верхней и идя по спирали (дойдя до края или уже закрашенной части, поворачивают направо, рис. 2). Какая клетка будет закрашена последней? (Укажите номер её строки и столбца. Например, нижняя правая клетка стоит в 100-й строке и 200-м столбце.)
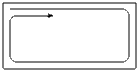
(A. Хачатурян)
Решение: =1Ответ: клетка, расположенная в строке 51 и столбце 50. Сначала будет закрашен наружный слой клеток, после чего останется прямоугольник 98 × 198 клеток. Этот прямоугольник также будет закрашиваться по спирали; после покраски его наружного слоя останется прямоугольник 96 × 196 клеток и так далее. После окраски 49 слоёв незакрашенным останется прямоугольник 2 × 102, расположенный в строках 50–51 и столбцах 50–151. Последней будет закрашена нижняя левая клетка этого прямоугольника.
Задача 2:
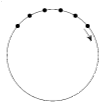
Можно ли поставить на плоскости 100 точек (сначала первую, потом вторую и так далее до сотой) так, чтобы никакие три точки не лежали на одной прямой и чтобы в любой момент фигура, состоящая из уже поставленных точек, имела ось симметрии?
(И. Акулич)
Решение: =2Ответ: да. Можно, например, ставить точки на окружности через равные достаточно малые интервалы (как на рисунке, только меньшие).
Задача 3:
Даны шесть слов:
ЗАНОЗА
ЗИПУНЫ
КАЗИНО
КЕФАЛЬ
ОТМЕЛЬ
ШЕЛЕСТ
За один шаг можно заменить любую букву в любом из этих слов на любую другую (например, за один шаг можно получить из слова ЗАНОЗА слово ЗКНОЗА. Сколько шагов нужно, чтобы сделать все слова одинаковыми (допускаются бессмысленные)? Приведите пример и докажите, что меньшим числом шагов обойтись нельзя.
(В. Доценко, А. Шень)
Решение: =3Ответ: 25. Напишем слова в столбик:
ЗАНОЗА ЗИПУНЫ КАЗИНО КЕФАЛЬ ОТМЕЛЬ ШЕЛЕСТ
После всех замен буквы в каждой колонке должны стать одинаковыми. Число замен будет наименьшим, если в каждой колонке сохранить наиболее частую букву (любую из них, если таких букв несколько). Например, в первой колонке можно оставить буквы З или К, они обе требуют четырёх замен. Минимальное число замен равно 4 + 4 + 5 + 4 + 4 + 4 = 25. Среди слов, которые могут получиться в результате, есть осмысленные, например ЗЕЛЕНЬ, КАПЕЛЬ или КАФЕЛЬ.
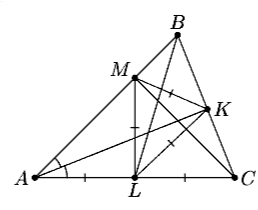
Задача 4:В треугольнике ABC проведены биссектриса AK, медиана BL и высота CM. Треугольник KLM равносторонний. Докажите, что треугольник ABC равносторонний.
(Р. Женодаров)
Решение: =4Напомним, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна её половине и, наоборот, если медиана равна половине стороны, к которой она проведена, то треугольник прямоугольный.
Медиана ML прямоугольного треугольника AMC равна половинам гипотенузы AL и LC, а также отрезкам KL и KM, так как стороны треугольника KLM равны (см. рис.). В треугольнике AKC медиана KL равна половине стороны AC, поэтому угол AKC прямой и в треугольнике ABC биссектриса AK является высотой. Следовательно, треугольник ABC равнобедренный (AB = BC) и AK является также медианой: BK = KC. Значит, MK – медиана прямоугольного треугольника BMC, поэтому BC = 2MK = 2KL = AC. Итак, AB = BC = AC, что и требовалось доказать.
Задача 5:
Лёша задумал двузначное число (от 10 до 99). Гриша пытается его отгадать, называя двузначные числа. Считается, что он отгадал, если одну цифру он назвал правильно, а в другой ошибся не более чем на единицу (например, если задумано число 65, то 65, 64 и 75 подходят, а 63, 76 и 56 – нет). Придумайте способ, гарантирующий Грише успех за 22 попытки (какое бы число ни задумал Лёша).
(Фольклор)
Решение:Расположим двузначные числа в клетках прямоугольника высоты 9 и ширины 10 (по горизонтали откладываем единицы, по вертикали – десятки).
Каждой попытке Гриши соответствует крестик из пяти клеток: в центре названное им число, а по бокам четыре числа, отличающиеся в одной цифре на единицу (если названное число содержит цифру 0 или 9, некоторые клетки крестика выходят за края прямоугольника; таким клеткам никакие числа не соответствуют). Задача Гриши – покрыть прямоугольник 9 × 10 такими крестиками. Убедимся, что 22 крестиков ему хватит.
Покрытие из 22 крестиков легко найти, если заметить, что крестиками можно выложить плоскость без перекрытий (правда, придётся ещё добавить несколько крестиков по краям прямоугольника). Например, Гриша может назвать числа 11, 13, 17, 25, 29, 30, 32, 37, 44, 49, 51, 56, 63, 68, 70, 75, 82, 87, 89, 90, 94, 97.
Задача 6:Лёша задумал двузначное число (от 10 до 99). Гриша пытается его отгадать, называя двузначные числа. Считается, что он отгадал, если одну цифру он назвал правильно, а в другой ошибся не более чем на единицу (например, если задумано число 65, то 65, 64 и 75 подходят, а 63, 76 и 56 – нет). Покажите, что нет способа, гарантирующего Грише успех за 18 попыток.
(Фольклор)
Решение:Расположим двузначные числа в клетках прямоугольника высоты 9 и ширины 10 (по горизонтали откладываем единицы, по вертикали – десятки).
Каждой попытке Гриши соответствует крестик из пяти клеток: в центре названное им число, а по бокам четыре числа, отличающиеся в одной цифре на единицу (если названное число содержит цифру 0 или 9, некоторые клетки крестика выходят за края прямоугольника; таким клеткам никакие числа не соответствуют). Задача Гриши – покрыть прямоугольник 9*10 такими крестиками. Убедимся, что 18 крестиков ему не хватит.
Суммарная площадь крестиков равна 18 × 5 = 90, т.е. равна площади прямоугольника. Но, покрывая угловую клетку, мы неизбежно выйдем за пределы прямоугольника, и эта потеря помешает покрыть весь прямоугольник.
| Задачная база >> Московские соревнования >> Городская олимпиада >> 2001 >> Городской тур >> 8 класс | Убрать решения |