Задача 1:
Фокусник угадывает поочередно масть всех карт в колоде из 52 карт.
После каждого ответа ему сообщают, угадал он или ошибся. Докажите, что
существует стратегия, позволяющая угадать не менее 13 карт, и нет стратегии,
позволяющей гарантированно угадать больше.
Задача 2:
Внутри треугольника ABC взята точка O. Обозначим
через A
1, B
1, C
1 проекции
точки O на прямые BC, CA, AB соответственно. Через
A
2, B
2, C
2 обозначим
вторые точки пересечения прямых AO, BO, CO с описанной
окружностью треугольника ABC. Докажите, что треугольники
A
1B
1C
1 и
A
2B
2C
2 подобны.
Задача 3:
Докажите, что неравенство
|x! – y
y| ≤ n при любом натуральном
n имеет лишь конечное число решений в натуральных числах x,
y.
Задача 4:
Найдите для каждого натурального n ≥ 1 все функции (не
обязательно непрерывные), которые удовлетворяют уравнению
f(x + y) = f
n(x) + f
n(y).
Задача 5:
Дано k последовательностей s
1, …,
s
k длины n, состоящих из ± 1. Докажите,
что можно найти такую последовательность s, состоящуюю из ± 1,
что количество последовательностей, принадлежащих одновременно обоим
множествам
s
1, … ,s
k и
ss
1, … ,ss
k не
превосходит
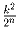
. (Произведением
последовательностей x
i и
y
i называется последовательность
x
iy
i.)
Задача 6: Прямые разбивают верхнюю полуплоскость на многоугольники, диаметр
каждого из которых меньше 1, и все стороны и площадь больше 0.000001. Докажите,
что один из них можно выдвинуть вниз, не смещая остальные.


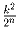 . (Произведением
последовательностей xi и
yi называется последовательность
xiyi.)
Задача 6:
. (Произведением
последовательностей xi и
yi называется последовательность
xiyi.)
Задача 6: