 |
 |
|
| Задачная база >> Московские соревнования >> Городская олимпиада >> 2002 >> Окружной тур >> 10 класс. Центральный округ | Убрать решения |
|
|
| 65 Московская математическая олимпиада. Окружной тур. 10 класс. Центральный округ |
|
|
Задача 2: Существует ли треугольник длины высот которого равны числам 1, 2 и 3?
Задача 3: Двузначное число, у которого число единиц больше числа десятков умножили на 9. Найти сумму цифр полученного числа.
Задача 4: Сравнить два числа
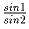 и
и
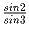 .
.Задача 5: Задача 6: Существуют ли натуральные числа x и y, при которых выражение 2x² + 3xy + y² принимает значение 3²ºº²?
| Задачная база >> Московские соревнования >> Городская олимпиада >> 2002 >> Окружной тур >> 10 класс. Центральный округ | Убрать решения |