Задача 1: 2.
Задача 3:
Написано несколько положительных чисел, каждое из которых равно
полусумме остальных. Сколько написано чисел?
Задача 4:
Центры двух единичных кубов совпадают. Доказать, что при любом
взаимном положении объем общей части не меньше
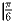
.
Задача 5:
В траншею, имеющую в сечении форму параболы
y = x², требуется уложить трубу круглого сечения так,
чтобы она касалась дна траншеи. При каком наибольшем радиусе трубы это
возможно?
Задача 6:
Найти непрерывную на
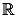
функцию, такую, что для любых
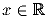
, y ∈ R справедливы равенства
f(x + y) = f(x) + f(y) + xy и f(1) = 1.


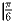 .
.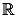 функцию, такую, что для любых
функцию, такую, что для любых
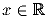 , y ∈ R справедливы равенства
f(x + y) = f(x) + f(y) + xy и f(1) = 1.
, y ∈ R справедливы равенства
f(x + y) = f(x) + f(y) + xy и f(1) = 1.