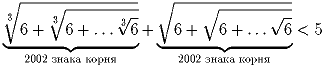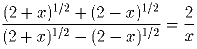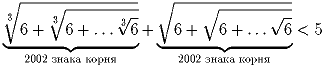Задача 1:
Решите уравнение
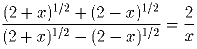
Задача 2:
Существует ли многогранник, у которого ровно 13 рёбер?
Задача 3:
Что больше:
2001 + sin 2001 или 2002 + sin 2002?
Задача 4:
Из вершин C и D ромба ABCD с острым
углом A на прямую AB опущены перпендикуляры CQ и
DP. Точки M и N – середины отрезков PB и
CQ соответственно.
Докажите, что AN ⊥ DM.
Задача 5:
В траншею, имеющую в сечении форму параболы
y = x², требуется уложить трубу круглого сечения
так, чтобы она касалась дна траншеи. При каком наибольшем радиусе трубы
это возможно?
Задача 6:
Докажите неравенство