Задача 1: (6) Можно ли в прямоугольной таблице 5 × 10 так расставить числа, чтобы сумма чисел любой строки равнялась бы 30, а сумма чисел любого столбца равнялась бы 10,?

Решение: Предположим, что такая таблица существует, и подсчитаем, чему равняется сумма всех ее чисел. С одной стороны, таблица содержит 5 строк, сумма чисел в каждой из которых — 30, значит искомая сумма равна 150. С другой стороны, в таблице 10 столбцов, сумма чисел в каждом из которых — 10. Отсюда общая сумма равна 100. Полученное противоречие показывает, что такой таблицы не существует.

Задача 2: (6) Сумма нескольких чисел равна 1. Может ли сумма их квадратов быть меньше 0.1,?

Решение: Условию задачи удовлетворяют одиннадцать чисел, равных 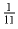. Их сумма равна .

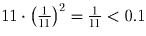Задача 3: (6–8) а) Назовите 10 первых натуральных чисел, имеющих нечетное число делителей (в число делителей включается единица и само число);

б) попробуйте сформулировать и доказать правило, позволяющее найти следующие такие числа.

Решение: Если x — делитель числа A, то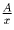 — тоже его делитель. Это простое наблюдение показывает, что каждому делителю числа A можно поставить в соответствие двойственный делитель (так, что произведение любого делителя на свой двойственный равно A). При этом очевидно, что делитель x является двойственным себе тогда и только тогда, когда x² = A. Таким образом, если число A не является полным квадратом, то все его делители разбиваются на пары двойственных друг другу, тем самым их количество четно. Если же число A является полным квадратом, то при разбиении его делителей на пары двойственных без пары останется единственный делитель 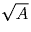. Значит, в этом случае количество делителей нечетно. Итак, натуральное число имеет нечетное число делителей тогда и только тогда, когда оно является полным квадратом. Первые десять таких чисел — 1, 4, 9, 16, 25, 36, 49, 64, 81, 100.

Задача 4: (7–8) а) Показать, что любой треугольник можно разрезать на несколько частей, из которых можно сложить прямоугольник;

б) показать, что любой прямоугольник можно разрезать на несколько частей, из которых можно сложить квадрат;

в) верно ли, что любой многоугольник можно разрезать на несколько частей, из которых можно сложить квадрат?

Решение: а) Равносоставленность (см. Т15) любого треугольника и некоторого прямоугольника следует из рис. 4 (прямая l на рисунке содержит среднюю линию треугольника).

б) Докажем сначала, что любой параллелограмм равносоставлен прямоугольнику, одна сторона которого равна основанию параллелограмма, а другая — его высоте. Если высота параллелограмма падает на его основание, то его нужно разрезать по высоте (рис. 5).

Если же она падает на продолжение основания, то тогда линиями, параллельными основанию, параллелограмм можно разрезать на параллелограммы, у которых высоты падают на основания. После этого каждый из полученных параллелограммов можно разрезать описанным выше способом (рис. 6). (Дотошный читатель сообразит, что последней оговорки можно было бы и не делать, поскольку всегда по крайней мере одна из высот параллелограмма падает на основание, а не на его продолжение; попробуйте доказать это самостоятельно.)

Теперь перейдем к доказательству основного утверждения пункта б). Для любого прямоугольника можно найти параллелограмм, у которого:

1) большая сторона равна большей стороне прямоугольника;

2) высота, опущенная на большую сторону, равна меньшей стороне прямоугольника;

3) меньшая сторона равна опущенной на нее высоте.

Способ построения такого параллелограмма приведен на рис. 7.

Согласно доказанному утверждению, этот параллелограмм равносоставлен как исходному прямоугольнику, так и квадрату со стороной, равной его меньшей стороне. Значит, исходный прямоугольник равносоставлен квадрату.

в) Докажем, что любой многоугольник можно разрезать на треугольники. Если многоугольник выпуклый, это очевидно — достаточно провести все диагонали из одной вершины. Если же он не выпуклый, то его можно разрезать на выпуклые, проведя продолжения всех его сторон. Согласно пунктам а) и б), каждый треугольник равносоставлен некоторому квадрату. Осталось доказать, что произвольные несколько квадратов можно разрезать на части, из которых можно сложить один квадрат. Как это сделать для двух квадратов, показано на рис. 8. Если квадратов больше двух, то проделав эту операцию с любыми двумя, мы уменьшим их количество на один. Повторяя ее, мы получим в конце концов один квадрат.