Задача 1:
(6–7)
Из утверждений «число a делится на 2", «число a делится
на 4", «число a делится на 12" и «число a делится на 24" три
верных, а одно неверное. Какое?
Решение:
Предположим, что последнее утверждение верно. Но в
этом случае будут верными также и первые три утверждения, так как
если число делится на 24, то оно также делится на 2, 4 и 12.
Поэтому последнее утверждение не может быть верным.
Покажем теперь, что ситуация, когда первые три утверждения
верны, а последнее — нет, возможна. Эта ситуация реализуется,
например, если a = 12.
Задача 2:
(6–7)
На доске написаны числа 0, 1, 0, 0. За один шаг разрешается
прибавлять единицу к любым двум из них. Можно ли, повторяя эту
операцию, добиться, чтобы все числа стали равными?
Решение:
За каждый шаг, независимо от того, какие числа мы
увеличиваем, сумма всех написанных чисел увеличивается на 2.
Поскольку вначале сумма равна 1, то она всегда будет оставаться
нечетной. А сумма четырех одинаковых чисел, очевидно, четна.
Поэтому, добиться, чтобы все числа стали равными невозможно.
Задача 3:
(6–7)
Несколько ящиков вместе весят 10 тонн, причем каждый из
них весит не более одной тонны. Сколько трехтонок заведомо
достаточно, чтобы увезти этот груз?
Решение:
Покажем, что пяти машин заведомо достаточно. Будем
грузить машины ящиками в любом порядке до тех пор, пока ящики не
кончатся, следя лишь за тем, чтобы не наступила «перегрузка"
машины. Это возможно, так как в любой момент погрузки будет хотя
бы одна машина, загруженная не более чем двумя тоннами.
Действительно, если бы все машины были загружены больше, чем на
две тонны, то общий вес груза составлял бы больше, чем
5 • 2,т=10,т, что противоречит условию задачи. Эту машину
можно догрузить любым ящиком, поскольку по условию задачи он весит
не более тонны. Осталось показать, что четырех машин может не
хватить. Например, для вывоза 13 ящиков весом
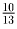
,т каждый, четырех машин недостаточно.
Действительно, каждая машина может увезти не более трех таких
ящиков, так как четыре ящика весят
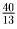
,т > 3,т. Значит, все машины
увезут не больше 12 ящиков.


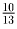 ,т каждый, четырех машин недостаточно.
Действительно, каждая машина может увезти не более трех таких
ящиков, так как четыре ящика весят
,т каждый, четырех машин недостаточно.
Действительно, каждая машина может увезти не более трех таких
ящиков, так как четыре ящика весят
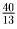 ,т > 3,т. Значит, все машины
увезут не больше 12 ящиков.
,т > 3,т. Значит, все машины
увезут не больше 12 ящиков.