 |
 |
|
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1984 | Убрать решения |
|
|
| Турнир имени Ломоносова. Конкурс по математике. 1984 |
|
|
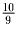 ,руб.=1,руб. 11
,руб.=1,руб. 11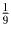 ,коп.
Аналогично,
второе условие равносильно тому, что 1,кг ирисок стоит дороже, чем
,коп.
Аналогично,
второе условие равносильно тому, что 1,кг ирисок стоит дороже, чем
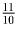 ,руб.=1,руб. 10,коп. Поэтому ответом в
задаче является любая сумма, большая 1,руб. 10,коп. и меньшая
1,руб. 11
,руб.=1,руб. 10,коп. Поэтому ответом в
задаче является любая сумма, большая 1,руб. 10,коп. и меньшая
1,руб. 11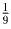 ,коп. Естественно, что цена килограмма
ирисок выражается целым числом копеек. Поэтому ответ однозначен:
1,руб. 11,коп.
,коп. Естественно, что цена килограмма
ирисок выражается целым числом копеек. Поэтому ответ однозначен:
1,руб. 11,коп.Задача 2: (5–7) Петя написал на гранях кубика натуральные числа от 1 до 6. Вася кубика не видел, но утверждает, что
а) у этого кубика есть две соседние грани, на которых написаны соседние числа;
б) таких пар соседних граней у кубика не меньше двух.
Прав ли он в обоих случаях? Почему?
Решение: В наборе натуральных чисел от 1 до 6 можно найти пять пар соседних чисел: 1 и 2, 2 и 3, 3 и 4, 4 и 5, 5 и 6. Каждая такая пара может быть написана либо на двух соседних гранях кубика, либо на двух противоположных. Но пар противоположных граней у кубика всего три. Поэтому их могут занимать не более трех пар соседних чисел. Значит, по крайней мере две такие пары занимают соседние грани. Следовательно, можно утверждать, что Вася прав в обоих случаях.Задача 3: (5–7) Можно ли разлить 50,л бензина по трем бакам так, чтобы в первом баке было на 10,л больше, чем во втором, а после переливания 26,л из первого бака в третий в третьем баке стало столько же, сколько во втором? Решение: Из второго условия задачи следует, что в каждом из двух баков — первом и втором должно быть не меньше 26,л бензина. Действительно, поскольку из первого бака можно перелить 26,л, то, очевидно, изначально в нем должно было быть не меньше 26,л. Кроме того, после такого переливания в третьем баке будет не меньше 26,л, а по условию это столько же, сколько во втором. Поэтому общий объем бензина в первых двух баках должен быть не меньше 52,л. Поэтому даже одного второго условия достаточно, чтобы утверждать, что такой разлив осуществить невозможно.
Задача 4: (8–9) Можно ли провести из одной точки на плоскости пять лучей так, чтобы среди образованных ими углов было ровно четыре острых? Рассматриваются углы не только между соседними, но и между любыми двумя лучами. Решение: Требуемое расположение приведено на рис. 13.
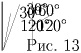
Задача 5: (8–9) У куба отмечены вершины и центры граней, а также проведены диагонали всех граней. Можно ли по отрезкам этих диагоналей обойти все отмеченные точки, побывав в каждой из них ровно один раз? Решение: Мы имеем отмеченные точки двух типов: вершины и центры граней. Отрезки диагоналей граней соединяют попарно точки разных типов. Поэтому, проходя по этим отрезкам, мы будем встречать отмеченные точки в порядке чередования их типов, т.е. если мы в некоторый момент встретим вершину, то в следующий момент встретим центр грани, и наоборот. Из этого следует, что в любой момент либо количества пройденных точек обоих типов равны, либо точек одного типа на одну больше, чем другого. Мы же имеем 8 вершин и 6 центров граней — точек одного типа на 2 больше, чем точек другого типа. Поэтому требуемый обход осуществить невозможно.
Задача 6: (8–9) Автобусные билеты имеют номера от 000000 до 999999. Билет называется счастливым, если сумма первых трех цифр его номера равна сумме последних трех его цифр. Докажите, что:
а) число всех счастливых билетов четно;
б) сумма номеров всех счастливых билетов делится на 999.
Решение: Как можно пытаться доказать, что количество счастливых билетов четно? Можно стараться подсчитать это количество. В принципе, эта задача вполне разрешима, однако она гораздо сложнее предложенной. Другой естественный способ — постараться разбить все счастливые билеты на пары. Мы укажем два способа такого разбиения.
Первый способ. Переставим в номере билета первые три цифры с последними тремя цифрами. Полученный билет и поставим в пару исходному (например, билету 239671 парой будет 671239). Очевидно, что этот билет также будет счастливым и парой к нему является исходный билет. Так мы разбили на пары все билеты кроме тех, которые являются парными сами к себе. Это билеты, для которых первые три цифры номера совпадают с последними тремя цифрами (все такие билеты счастливые). Сколько таких билетов? Их ровно 1000. Действительно, первые три цифры их номера могут образовывать любое трехзначное число от 000 до 999 (всего 1000 возможностей), при этом оставшиеся три цифры однозначно определяются первыми тремя (а именно, должны их в точности повторять). Итак, мы имеем какое-то количество счастливых билетов, разбитых на пары (оно очевидно четное), и еще 1000 билетов, пары не получивших. Значит, общее число счастливых билетов четно. Пункт a) доказан.
Второй способ. Этот способ поможет нам также доказать пункт б). Каждому счастливому билету поставим в соответствие билет, номер которого состоит из цифр, дополняющих соответствующие цифры номера исходного билета до девятки. Например, билет 239601 получит в пару билет 760398. Из равенства сумм троек цифр следует равенство сумм их дополнений до девятки, поэтому парой к каждому счастливому билету является также счастливый билет. Очевидно, что если билет A получает в пару билет B, то и наоборот, билет B получает в пару билет A. При этом никакой билет не получает в пару себя, так как в этом случае каждая цифра его номера должна была бы дополнять до девятки самое себя, что невозможно, поскольку 9 — нечетное число. Таким образом, мы получили разбиение всех счастливых билетов на пары. При этом сумма номеров билетов любой пары равна 999999, значит, она делится на 999. Сложив эти попарные суммы, получим число, делящееся на 999. С другой стороны, это будет сумма номеров всех счастливых билетов.
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1984 | Убрать решения |