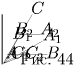Задача 1: (7–9) На сторонах шестиугольника было записано шесть чисел, а в каждой вершине — число, равное сумме двух чисел на смежных с ней сторонах. Затем все числа на сторонах и одно число в вершине стерли. Можно ли восстановить число, стоявшее в вершине?

Решение:

Пусть ABCDEF — данный шестиугольник, и нам нужно восстановить число в вершине A. Заметим, что сумма чисел в вершинах A, C и E равна сумме цифр в вершинах B, D и F. Действительно, обе эти суммы равны сумме чисел, стоявших исходно на всех сторонах шестиугольника. Поэтому, чтобы восстановить число в вершине A нужно из суммы чисел в вершинах B, D и F вычесть числа в вершинах C и E.

Задача 2: (7–9) Вершины A, B, C треугольника соединены с точками A₁, B₁, C₁, лежащими на противоположных сторонах (не в вершинах). Могут ли середины отрезков AA₁, BB₁, CC₁ лежать на одной прямой?

Решение:

Средняя линия B₂C₂ треугольника ABC параллельна основанию BC. Отсюда следует, что середина отрезка AA₁ лежит на отрезке B₁C₁. Это легко выводится из подобия треугольников (можно также применить теорему Фалеса). Аналогично, середины отрезков BB₁ и CC₁ лежат на двух других средних линиях треугольника ABC (рис. 44). Поскольку прямая не может пересекать три стороны треугольника во внутренних точках, три указанные точки не могут лежать на одной прямой.

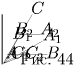
Задача 3: (7–9) Три шахматиста A, B и C сыграли матч-турнир (каждый с каждым сыграл одинаковое число партий). Может ли случиться, что по числу очков A занял первое место, C — последнее, а по числу побед, наоборот, A занял последнее место, C — первое (за победу присуждается одно очко, за ничью — пол-очка)?

Решение:

Описанная ситуация могла произойти, например, в следующем случае. Турнир проходил в 8 туров. A победил B 1 раз, а C — 2 раза; B победил C 4 раза, а A — ни разу; C победил A 2 раза, а B — 3 раза. Таким образом A одержал 3 победы и получил 8.5 очков, B — 4 победы и 8 очков, C — 5 побед и 7.5 очков.