 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1969 | Убрать решения |
|
|
| Канадская математическая олимпиада.. 1969 |
|
|
a1/b1 = a2/b2 = a3/b3. Докажите, что для любых p1,p2,p3 не равных нулю и любого натурального n
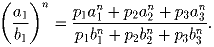
Определите, какое из следующих чисел 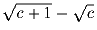 или
или 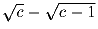 больше при всех c ≥ 1.
больше при всех c ≥ 1.
Решение:
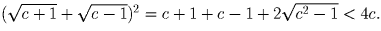
Докажите, что 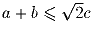 , где a и b – катеты, а c – гипотенуза прямоугольного треугольника.
Когда достигается равенство?
, где a и b – катеты, а c – гипотенуза прямоугольного треугольника.
Когда достигается равенство?
Внутри равностороннего треугольника ABC выбрали точку P. Докажите, что
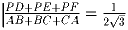 , где D,E и F – основания перпендикуляров,
опущенных из точки P на стороны треугольника.
, где D,E и F – основания перпендикуляров,
опущенных из точки P на стороны треугольника.
Докажите, что длина биссектрисы CD равна 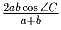 , где a = BC,
а b = AC.
, где a = BC,
а b = AC.
Найдите сумму 1 • 1! + 2 • 2! + 3 • 3! + … + n • n!
Решение:
k • k! = (k + 1)! – k!. откуда 1 • 1! + 2 • 2! + 3 • 3! + … + n • n! = 2! – 1! + 3! – 2! + 4! – 3! + … + (n + 1)! – n! = (n + 1)! – 1
Задача 7:Докажите, что уравнение a² + b² – 8c = 6 не имеет решений в целых числах.
Решение:
При делении на 8 квадраты натуральных чисел дают остатки 0, 1 или 4. Тогда, сумма двух квадратов (следовательно и a² + b² – 8c) не может давать остатка 6 при делении на 8.
Задача 8:
Строго монотонная функция f, определенная на множестве натуральных чисел и принимающая натуральные значения удовлетворяет следующим условиям: f(2) = 2 и f(mn) = f(m)f(n) для всех m и n. Докажите, что f(n) = n.
Решение:
Заметим, что f(2n) = 2n для любого n. Пусть 2n < k ≤ 2n + 1. Если f(k) > k, то и f(2n + 1) > 2n + 1, а если f(k) < k, то и f(2n) < 2n.
Задача 9:Докажите, что длина наименьшей стороны четырехугольника вписанного в окружность радиуса 1 не
превосходит 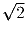 .
.
Из точки P на гипотенузезе равнобедренного прямоугольного треугольника ABC с катетом 1 ( ∠ C = 90) опустили перпендикуляры на стороны PQ и PR. Докажите, что по крайней мере одна площадь SAPQ, SBPR и SPQCR не менее 2/9.
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1969 | Убрать решения |