 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1975 | Убрать решения |
|
|
| Канадская математическая олимпиада.. 1975 |
|
|
Упростите выражение
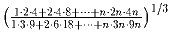
Решение:
2/3
Задача 2:a1 = 1/2, a1 + a2 + … + an = n²an. Найдите an
Решение:
Очевидно, что 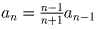 , откуда
, откуда 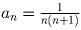 .
.
Найдите множество точек плоскости координаты которых удовлетворяют уравнению [x]² + [y]² = 4 ([x] – целая часть x).
Задача 4:Найдите положительное число, которое образует геометрическую прогрессию вместе со своей целой и дробной частями.
Задача 5:На окружности выбрали точки A,B,C,D (в таком порядке). P,Q,R,S – середины хорд AB,BC,CD,DA соответственно. Докажите, что PR и QS перпендикулярны.
Задача 6:На столе стоит 15 табличек с именами гостей. когда гости расселись, они обнаружили, что никто из них не сидит напротив таблички со своим именем. Докажите, что стол можно повернуть так, что напротив по крайней мере двух гостей будут таблички с их именами. Приведите пример рассадки гостей, такой, что при любом повороте стола не более 1 гостя сидит напротив своей таблички.
Задача 7:Является ли функция sin (x²) периодической или нет?
Задача 8:Найдите все многочлены P(x) с вещественными коэффициентами, которые удовлетворяют условию P(P(x)) = (P(x))k.
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1975 | Убрать решения |