 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1982 | Убрать решения |
|
|
| Канадская математическая олимпиада.. 1982 |
|
|
A1A2A3A4 – выпуклый четырехугольник, O – произвольная точка
плоскости. Построили точки B1,B2,B3,B4 такие,что
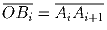 (A5 = A1). Докажите, что площадь
четырехугольника B1B2B3B4 в два раза больше площади
A1A2A3A4.
(A5 = A1). Докажите, что площадь
четырехугольника B1B2B3B4 в два раза больше площади
A1A2A3A4.
Решение:
Достаточно заметить, что площадь треугольника OBiBi + 1 равна площади треугольника AiAi + 1Ai + 2.
Задача 2:
a,b,c – корни уравнения x³ – x² – x – 1 = 0. Докажите, что a,b и c – различны, и число
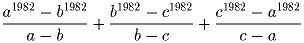
Задача 3:
Определите наименьшее количество точек, которое можно выбрать в
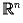 так, чтобы любая точка
так, чтобы любая точка 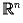 находилась на
иррациональном расстоянии по крайней мере от одной выбранной точки.
находилась на
иррациональном расстоянии по крайней мере от одной выбранной точки.
Задача 4:
Докажите, что количество перестановок из n элементов не имеющих неподвижных точек отличается от количества перестановок имеющих ровно одну неподвижную точку на 1.
Задача 5:
На продолжениях высот тетраэдра ABCD взяли точки A′,B′,C′,D′ такие, что они лежат вне тетраэдра и AA′ = k/ha, BB′ = k/hb, CC′ = k/hc, DD′ = k/hd, где k – произвольное число, ha – длина высоты опущенной из вершины A. Докажите, что центры тетраэдров ABCD и A′B′C′D′ совпадают.
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1982 | Убрать решения |