 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1984 | Убрать решения |
|
|
| Канадская математическая олимпиада.. 1984 |
|
|
Докажите, что сумма 1984 последовательных натуральных чисел не может быть точным квадратом.
Решение:
Сумма чисел от n + 1 до n + 1984 равна ½((n + 1984)(n + 1985) – n(n + 1)) = 992(2n + 1985), что делится на 32, но не делится на 64
Задача 2:
В какое наименьшее количество цветов нужно раскрасить n ключей так, чтобы не путать их между собой, если все n ключей находятся одном кольце?
Задача 3:
Докажите, что существует бесконечно много натуральных чисел, ни одна цифра которых не равна 0, и которые делятся на сумму своих цифр.
Решение:
Число, записанное при помощи 3n единиц делится на 3n.
Задача 4:
Площадь остроугольного треугольника равна 1. Докажите, что внутри
треугольника найдется точка такая, что расстояние от нее до каждой
вершины не более 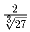 .
.
Решение:
Докажем, что радиус окружности, описанной вокруг данного треугольника
не больше 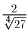 . Среди треугольников, вписанных в
данную окружность максимальную площадь имеет равносторонний
треугольник, площадь которого –
. Среди треугольников, вписанных в
данную окружность максимальную площадь имеет равносторонний
треугольник, площадь которого – 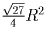 ,
следовательно среди треугольников единичной площади максимальный
радиус описанной окружности имеет равносторонний треугольник и дл
него он равен
,
следовательно среди треугольников единичной площади максимальный
радиус описанной окружности имеет равносторонний треугольник и дл
него он равен 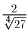 .
.
Задача 5:
Дано 7 вещественных чисел. Докажите, что среди них найдутся два числа x и y такие, что
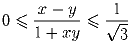
Решение:
Заметим, что 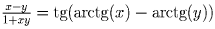 , но среди
арктангенсов 7 чисел по крайней мере два отличаются не более чем на
, но среди
арктангенсов 7 чисел по крайней мере два отличаются не более чем на
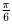 .
.
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1984 | Убрать решения |