Задача 1:

При каких значениях b уравнения 1988x² + bx + 8891 = 0 и 8891x² + bx + 1998 = 0 имеют общий корень?

Задача 2:

Вокруг дома, имеющего форму треугольника периметра P и площади S находится сад, который простирается на 5 метров от дома. Определите, какую площадь занимают дом и сад вместе.

Задача 3:

На плоскости расположено более 5 точек, некоторые из которых покрашены в красный цвет, остальные – в синий. Никакие три точки одного цвета не лежат на одной прямой. Докажите, что найдется треугольник все вершины которого одного цвета и по крайней мере одна сторона не содержит точек другого цвета.

Задача 4:

Последовательности x_n и y_n определены следующим образом: x₀ = 0,x₁ = 1,y₀ = 1,y₁ = 2, x_n + 1 = 4x_n – x_n – 1 и y_n + 1 = 4y_n – y_n – 1. Докажите, что .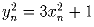

Задача 5:

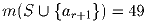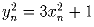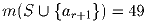S = a₁,a₂, … ,a_r. Для любого непустого подмножества A через p(A) обозначим произведение его элементов. m(S) = 13, где m(S) – среднее арифметическое p(A) по всем подмножествам S. Найдите a₁,a₂, … ,a_r,a_r + 1 если и все a_i – натуральные.