Задача 1: Докажите, что уравнение x² + y5 = z³ имеет бесконечно много решений
в ненулевых целых числах.
Задача 2:
Пусть n – фиксированное натуральное число.
Найдите сумму всех натуральных чисел,
в двоичная записи которых ровно n единиц и ровно n нулей.
Задача 3:
Пусть C – окружность, а P – некоторая точка плоскости.
Каждая прямая, проходящая через P и
пересекающая C, определяет некоторую хорду.
Докажите, что середины всех таких хорд лежат на одной окружности.
Задача 4:
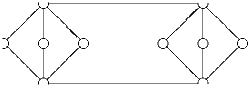
Из множества 0,1,2, … ,14 надо выбрать десять чисел и
заполнить ими круги на диаграмме. При этом все абсолютные значения разностей
чисел, оказавшихся на концах каждого отрезка должны быть попарно различны.
Возможно ли это?
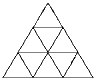
Задача 5:
На рисунке сторона большого равностороннего треугольника равна 3, а
f(3), количество параллелограммов со сторонами, идущими по линиям,
равно 15. По аналогии рассматривая более общую ситуацию, найдите формулу для
f(n), количества параллалограммов для треугольника со стороной n.