 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1995 | Убрать решения |
|
|
| Канадская математическая олимпиада.. 1995 |
|
|
Пусть 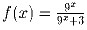 . Вычислите сумму
. Вычислите сумму
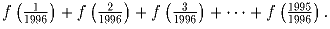
Задача 2:
a, b и c – положительные вещественные числа. Докажите, что
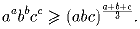
Бумерангом назовем четырехугольник без самопересечений, один из
углов которого больше 180 градусов. Выпуклый s-угольник
замостили q непересекающимися четырехугольниками, b из
которых – бумеранги. Докажите, что 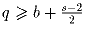 .
.
Задача 4:
n – некоторое натуральное число. Докажите, что для любого неотрицательного целого k уравнение
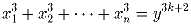
Задача 5:
Пусть u – вещественное число такое, что 0 < u < 1. Положим
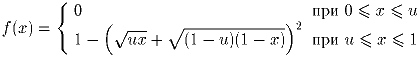
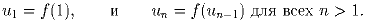
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1995 | Убрать решения |