 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1997 | Убрать решения |
|
|
| Канадская математическая олимпиада.. 1997 |
|
|
Определите количество пар натуральных чисел x,y с x ≤ y для которых (x,y) = 5!, а [x,y] = 50! ((x,y) – НОД, а [x,y] – НОК чисел x и y).
Решение:
Заметим, что решениями этой системы являются пары чисел:
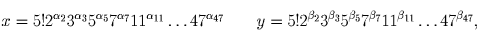
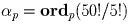 и β p = 0, либо наоборот.
Таким образом, количество решений равно 215.
и β p = 0, либо наоборот.
Таким образом, количество решений равно 215.Задача 2:
Отрезок [0,50] полностью покрыт отрезками длины 1. Докажите, что среди них можно выбрать несколько непересекающихся суммарной длины не менее 25.
Задача 3:Докажите, что
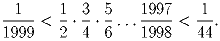
Внутри параллелограмма ABCD взяли точку O такую, что ∠ AOB + ∠ COD = 180. Докажите, что ∠ OBC = ∠ ODC.
Задача 5:Запишите сумму
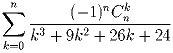
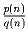 , где p и q – многочлены с целыми
коэффициентами.
, где p и q – многочлены с целыми
коэффициентами.
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1997 | Убрать решения |