 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 2000 | Убрать решения |
|
|
| Канадская математическая олимпиада.. 2000 |
|
|
В полдень Анна, Бет и Кармен начали бежать по круговой дорожке длиной триста метров, стартовав с одной точки. Каждая из них бежала с постоянной скоростью в одном из двух возможных направлений. Докажите, что, если скорость Анны отличается от скоростей двух других девочек, то в какой-то момент времени Анна будет на расстоянии не менее ста метров от каждой из соперниц (расстояние измеряется вдоль более короткой из двух дуг, разделяющих бегуний).
Решение:1 способ. Вращая систему координат, мы можем считать, что скорость Анны равна 0, Бет бежит не менее быстро, чем Кармен, а скорость Кармен положительна. Если Бет менее чем в два раза быстрее Кармен, то обе находятся на расстоянии не менее 100 метров от Анны в момент, когда Кармен пробежала 100 метров. Если Бет более чем в два раза быстрее Кармен, то Бет пробежала отрезок пути длиной более 200 метров, пока Кармен бежала межу 100-метровой и 200-метровой отметками. Некоторые части этого отрезка находятся на расстоянии более 100 метров от Анны, в это время и Бет и Кармен находятся на расстоянии не менее (а, на самом деле, более) 200 метров от Анны.
2 способ. Вращая систему координат, можно считать, что скорость Анны равна 0, а скорости Бет и Кармен не равны 0. Пусть Бет бежит не медленнее Кармен. Предположим, что Бет пробегает 200 метров за t секунд. Тогда в любой момент, принадлежащий бесконечному множеству T = t,2t,4t,8t, … , Бет будет на расстоянии ровно 100 метров от Анны. В момент времени t Кармен пробежала ровно d метров (0 ≤ d ≤ 200). Пусть k – наименьшее целое число такое, что 2kd ≥ 100. k ≥ 0 и 100 ≤ 2kd ≤ 200, поэтому в момент 2kt ∈ T и Бет и Кармен будут на расстоянии не менее 100 метров от Анны.
Комментарий: Организаторы были весьма удивлены сложностью этой задачи, средний балл за которую составил всего 1.43 (из 7). В работах участников встречался только первый способ решения.
Задача 2:
Перестановка чисел 1901,1902, … ,2000 – последовательность чисел a1,a2, … ,a100, в которой каждое из этих чисел встречается только один раз. Сфомируем последовательность частичных сумм такой перестановки:
s1 = a1,\;\;s2 = a1 + a2,\;\;s3 = a1 + a2 + a3,\; … \;,\;s100 = a1 + a2 + • s + a100.
Для скольких таких перестановок в последовательности s1, … ,s100 не будет членов, делящихся на 3?
Решение:Пусть 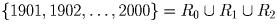 ,
где каждый элемент Ri сравним с i по модулю 3.
Заметим, что |R0| = |R1| = 33, а |R2| = 34. Каждая перестановка
S = (a1,a2, … ,a100) может быть единственным образом описана
последовательностью
S′ = (a1,a2, … ,a100) остатков по модулю 3
(содержащей 33 нуля, 33 единицы и 34 двойки) и тремя перестановками
элементов множеств R0, R1 и R2).
Заметим, что количество перестановок Ri в точтости равно
|Ri|! = 1 • 2 … |Ri|.
,
где каждый элемент Ri сравним с i по модулю 3.
Заметим, что |R0| = |R1| = 33, а |R2| = 34. Каждая перестановка
S = (a1,a2, … ,a100) может быть единственным образом описана
последовательностью
S′ = (a1,a2, … ,a100) остатков по модулю 3
(содержащей 33 нуля, 33 единицы и 34 двойки) и тремя перестановками
элементов множеств R0, R1 и R2).
Заметим, что количество перестановок Ri в точтости равно
|Ri|! = 1 • 2 … |Ri|.
Условие на частичные суммы S зависит только от последовательности
остатков S′. Для того, чтобы частичная сумма не делилась на 3,
подпоследовательность S′, образованная 67-ю единицами и двойками
должна быть или
1,1,2,1,2,...,1,2, или 2,2,1,2,1,...,2,1.
Поскольку |R2| = |R1| + 1, возможен только второй вариант.
33 нуля, входящие в S′ могут встретиться где угодно в
последовательности (a1′,a2′, … ,a100′) при условии, что
a1′ ≠ 0. Всего есть 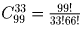 способов
выбрать нулевые элементы S′. Поэтому ровно у
способов
выбрать нулевые элементы S′. Поэтому ровно у 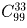 последовательностей S′ частичные сумм делятся на 3. Таким образом, общее
количество перестановок S, удовлетворяющих нашему требованию в точности
последовательностей S′ частичные сумм делятся на 3. Таким образом, общее
количество перестановок S, удовлетворяющих нашему требованию в точности
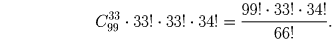
Комметарий: Эта задача оказалась самой простой и прямолинейной: средний балл за неё составил 3.07.
Задача 3: Пусть A = (a1,a2, … ,a2000) – последовательность целых чисел из промежутка [ – 1000,1000]. Предположим, что сумма элементов A равна 1. Докажите, что можно выбрать непустую подпоследовательность A, сумма элементов которой равна нулю.Задача 4:
Пусть ABCD – выпуклый четырёхугольник с
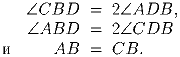
Предположим, что вещественные числа a1,a2, … ,a100 таковы, что
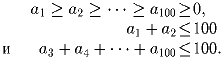
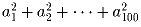 , и найдите все возможные
последовательности
a1,a2, … ,a100, для которых достигается этот максимум.
, и найдите все возможные
последовательности
a1,a2, … ,a100, для которых достигается этот максимум.
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 2000 | Убрать решения |