Задача 1: Бильярдный стол имеет форму прямоугольника вершины которого
находятся в точках O(0,0), A(0,1), 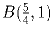 и
и
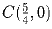 . Шар, начавший двигаться из точки P(0,⅓),
отражается прежде всего от борта AB стола в точке X. Двигаясь дальше,
шар отражается от бортов BC и CO и вернется в конце концов в исходную
точку P. Найти координаты точки X.
. Шар, начавший двигаться из точки P(0,⅓),
отражается прежде всего от борта AB стола в точке X. Двигаясь дальше,
шар отражается от бортов BC и CO и вернется в конце концов в исходную
точку P. Найти координаты точки X.
Задача 2: Показать, что уравнение 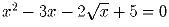 не имеет вещественных
решений.
не имеет вещественных
решений.
Задача 3: Найти все трехзначные числа 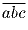 такие, что a,b,c ≠ 0 и
такие, что a,b,c ≠ 0 и
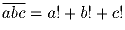 .
.
Задача 4: Пусть a,b,c – длины сторон треугольника и
α , β , γ – соответственно величины углов, расположенных
против этих сторон. Доказать, что если α = 2( β – γ ), то
a²b = (b + c)(b² – c²).
Задача 5: Пусть A – сумма первых n членов геометрической прогрессии
a1,a2, … и B – сумма обратных значений тех же членов.
Найти произведение первых n членов этой прогрессии.
Задача 6: На бесконечной клетчатой бумаге некоторые клетки отмечены, так что
любой прямоугольник, состоящий из 12 клеток содержит по крайней мере одну
отмеченную клетку. Доказать, что найдется прямоугольник, состоящий из 8
клеток и содержащий по крайней мере две отмеченные клетки.


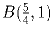 и
и
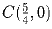 . Шар, начавший двигаться из точки P(0,⅓),
отражается прежде всего от борта AB стола в точке X. Двигаясь дальше,
шар отражается от бортов BC и CO и вернется в конце концов в исходную
точку P. Найти координаты точки X.
. Шар, начавший двигаться из точки P(0,⅓),
отражается прежде всего от борта AB стола в точке X. Двигаясь дальше,
шар отражается от бортов BC и CO и вернется в конце концов в исходную
точку P. Найти координаты точки X.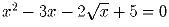 не имеет вещественных
решений.
не имеет вещественных
решений.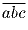 такие, что a,b,c ≠ 0 и
такие, что a,b,c ≠ 0 и
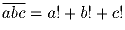 .
.