 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Эстонская МО >> 1996 >> 10 класс. Заключительный тур | Убрать решения |
|
|
| Национальные зарубежные олимпиады. Эстонская МО. 1996. 10 класс. Заключительный тур |
|
|
Найти все такие пары чисел (x,y), что сумма дробей 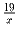 и
и
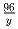 равна произведению этих же дробей.
равна произведению этих же дробей.
Какое число больше,
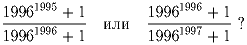
Имеется 1\,000\,000 куч по 1996 монет в каждой из них, причем в одной куче только фальшивые монеты, а во всех остальных – только настоящие. Каким наименьшим числом взвешиваний можно определить кучу, содержащую фальшивые монеты, если используемые весы имеют одну чашу и позволяют взвешивать сколь угодно большой вес с точностью до одного грамма, а также известно, что каждая фальшивая монета весит 9 граммов, а кажда настоящая – 10 граммов?
Задача 4:Пусть K, L, M и N – соответственно середины сторон CD, DA, AB и BC квадрата ABCD. Найти площадь общей части треугольников AKB, BLC, CMD и DNA, если сторона квадрата ABCD равна 1.
Задача 5:Юри и Мари хотят сыграть в следующую игру. В начале игры выбираются числа n > m ≥ 0 и на пустой стол кладется n конфет. Далее игроки начинают по очереди делать ходы. Каждый ход состоит в выборе неотрицательного целого числа k ≤ m и взятии со стола k конфет (в случае k = 0 игрок не делает ничего). При этом число k, выбранное игроком, не должно совпадать ни с одним из чисел, выбранных тем или другим игроком на каком-либо предыдущем ходе, а также не может превышать числа конфет на столе. Игра заканчивается, если один из игроков не может сделать очередной ход.
Юри и Мари решили, что сначала Мари выбирает числа n и m, а затем Юри решает, считать ли игрока, сделавшего последний ход, выигравшим или проигравшим. Первый ход делает Мари. Может ли она выбрать числа m и n так, чтобы иметь возможность выиграть игру независимо от решения Юри?
| Задачная база >> Национальные зарубежные олимпиады >> Эстонская МО >> 1996 >> 10 класс. Заключительный тур | Убрать решения |