Задача 1: a) В ряд записано 5 различных чисел. Верно ли, что всегда можно выбрать
из них 3 стоящих по возрастанию или по убыванию?
b) Тот же вопрос для выборки 4 чисел из 9.
Задача 2:
Задача 3: Докажите, что среднее арифметическое всех делителей числа n
лежит между 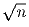 и
и 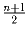 .
.
Задача 4: Найдите отношение длин сторон треугольника, если известно, что
вписанная окружность делит одну из его медиан на три равные части.
Задача 5: Функция f задана на отрезке [0,1] и принимает на нем неотрицательные значения.
Известно, что f(1) = 1 и для любых x1,x2 ∈ [0,1], если x1 + x2 ≤ 1,
то f(x1 + x2) ≥ f(x1) + f(x2). a) Докажите, что f(x) ≤ 2x для всех x.
b) Верно ли, что f(x) ≤ 1,9x для всех x?


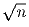 и
и 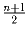 .
.