Задача 1: На стороне BC треугольника ABC взяли точку K. L – точка пересечения биссектрисы угла KAC и BC. Оказалось, что BC • KL = BK • CL. Докажите, что AL ⊥ AB.

Задача 2: Натуральное число n называется хорошим, если существуют n целых чисел сумма и произведение которых равны n. (Например, 8 = 4 • 2 • 1 • 1 • 1 • 1 • ( – 1) • ( – 1) = 4 + 2 + 1 + 1 + 1 + 1 + ( – 1) + ( – 1)). Докажите, что числа 4k + 1 (при k ≥ 0) и 4l (при l ≥ 2) являются хорошими.

Задача 3: Докажите, что среди любых 18 последовательных трехзначных чисел найдется по крайней мере одно, которое делится на сумму своих цифр.

Задача 4: Докажите, что ни при каком целом q уравнение x² + 7x – 14(q² + 1) = 0 не имеет целых корней.

Задача 5: a,b,c – стороны треугольника. Докажите, что

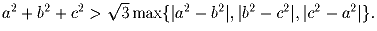
Задача 6: A₁A₂A₃ … A₂₁ – правильный 21-угольник с центром O. Найдите количество треугольников A_iA_jA_k, содержащих точку O.

Задача 7: Докажите, что x² sin x + x cos x + x² + ½ > 0.