Задача 1: В выпуклом четырехугольнике ABCD:  ∠ BAC = 50,  ∠ CAD = 60,  ∠ CBD = 30,  ∠ BDC = 25, E – точка пересечения диагоналей. Найдите  ∠ AEB.

Задача 2: Сумма квадратов n простых чисел, каждое из которых больше 5 делится на 6. Докажите, что и n тоже делится на 6.

Решение: Квадрат простого числа большего 5 сравним с 1 по модулю 6, следовательно, сумма квадратов таких простых чисел сравнима с их количеством.

Задача 3: Докажите, что для любого натурального n:

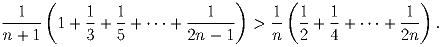
Задача 4: В равнобедренном треугольнике ABC угол при вершине равен 30. Точки A′,B′C′ получаются отражением вершин относительно противоположных сторон. Докажите, что треугольник A′B′C′ равносторонний.

Задача 5: Какое наименьшее значение может принимать 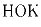20 не обязательно различных натуральных чисел с суммой 801.

Задача 6: Дано 7-элементное множество A. Придумайте набор троек элементов A такой, что любая пара элементов A принадлежит ровно одной тройке набора.