 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Ирландия >> 1993 | Убрать решения |
|
|
| Ирландская математическая олимпиада.. 1993 |
|
|
Вещественные числа α и β удовлетворяют уравнениям:
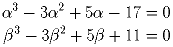
Натуральное число n называется хорошим если оно может быть единственным образом записано одновременно в виде суммы и произведения чисел a1,a2, … ,ak (например 10 – хорошее число, поскольку 10 = 5 + 2 + 1 + 1 + 1 = 5 • 2 • 1 • 1 • 1). Опишите в терминах простых чисел все хорошие натуральные числа.
Задача 3:Прямая l касается окружности S в точке A. B и C – точки на l лежащие по разные стороны от A. Касательные, проведенные из точек B и C к S пересекаются в точке P. найдите геометрическое место точек P при B и C меняющихся по прямой l при условии |AC| • |AB| = x, где x – некоторое положительное вещественное число.
Задача 4:Для многочлена f(x) = a0 + a1x + • s + an – 1xn с вещественными коэффициентами выполнено условие |f(0)| = f(1) и все его корни лежат в интервале (0,1). Докажите, что произведение корней не превосходит 1/2n.
Задача 5:Для комплексного числа z = x + iy (x,y – вещественные) через P(z) обозначим точку плоскости (x,y). Пусть z1,z2,z3,z4,z5, α – не равные нулю комплексные числа такие, что
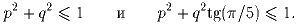
Дано пять точек на плоскости с целочисленными координатами. Докажите, что среди этих пяти точек найдутся две – P и Q такие, что середина отрезка PQ имеет также целочисленные координаты.
Задача 7:a1,a2, … ,an,b1,b2, … ,bn – 2n вещественных чисел, притом все числа ai – различны. Существует такое вещественное число α такое, что для любого i (ai + b1)(ai + b2) … (ai + bn) = α Докажите, что существует такое β , что для любого j (a1 + bj)(a2 + bj) … (an + bj) = β .
Задача 8:Обозначим через 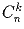 – биномиальный коэффициент (количество
способов выбрать k предметов из n). Положим
– биномиальный коэффициент (количество
способов выбрать k предметов из n). Положим 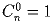 и
и 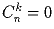 при
k > n. Докажите равенство:
при
k > n. Докажите равенство:
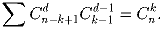
x – вещественное число из интервала (0, π ). Докажите, что дл любого натурального n следующая сумма положительна:
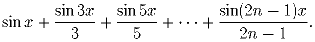
(a) Прямоугольник PQRS со сторонами |PQ| = l, |QR| = m, где m и n – натуральные числа, разделили на lm квадратиков 1 × 1 прямыми параллельными сторонам. Докажите, что диагональ PR пересекает l + m – d квадратиков, где d – наибольший общий делитель m и l.(b) Прямоугольный параллелепипед, ребра которого равны натуральным числам l,m и n разделили на lmn единичных кубиков. Сколько этих кубиков пересекает диагональ соединяющая вершину параллелепипеда с наиболее удаленной от нее?
| Задачная база >> Национальные зарубежные олимпиады >> Ирландия >> 1993 | Убрать решения |