Задача 1:

x,y – два натуральных числа, причем y > 3 и x² + y⁴ = 2((x – 6)² + (y + 1)²). Докажите, что x² + y⁴ = 1994.

Решение:

Перепишем условие в виде x² – 24x – y⁴ + 2y² + 4y + 74 = 0, откуда (x – 12)² = y⁴ – 2y² – 4y + 70. Заметим, что при y > 3: (y² – 2)² < y⁴ – 2y² – 4y + 70 < (y² + 1)², откуда, y⁴ – 2y² – 4y + 70 равняется либо (y² – 1)², либо y⁴. В первом случае получаем y = 69/4, во втором – y = 5, либо y =  – 7. Следовательно, y = 5, x = 37 и x² + y⁴ = 1994.

Задача 2:

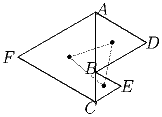
Точка B лежит на отрезке AC. Построили равносторонние треугольники ABD, BCE и CAF, при этом точки D и E лежат с одной стороны от прямой AC, а точка F – с другой. Докажите, что центры этих треугольников являются вершинами равностороннего треугольника, центр которого лежит на прямой AC.

Задача 3:

Найдите все многочлены f(x) с вещественными коэффициентами, удовлетворяющие уравнению f(x²) = f(x)f(x – 1).

Задача 4:

Сколько существует таблиц n × m, в каждой клетке которых записаны числа 0 или 1, обладающих свойством, что в каждом столбце и каждой строке количество единиц четно.

Задача 5:

Для каждого натурального n определим f(n) следующим образом:

Докажите, что для всех n > 1

Задача 6:

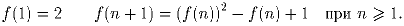
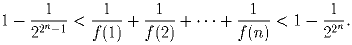
Последовательность x_n определена соотношениями:

Докажите, что x_n – целое для любого n.

Задача 7:

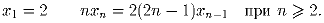
p,q и r – различные вещественные числа такие, что

Чему может равняться p + q + r?

Задача 8:

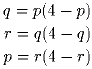
Докажите, что для любого целого n > 1

Задача 9:

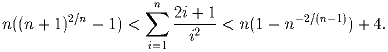
w,a,b,c – различные вещественные числа, для которых существуют такие x,y и z, что

Выразите w через a,b и c.

Задача 10:

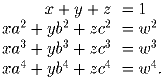
Какое максимальное количество отрезков можно провести в квадрате так, чтобы затем, разрезав по ним квадрат, получилось бы n выпуклых многоугольников?