 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Ирландия >> 1997 | Убрать решения |
|
|
| Ирландская математическая олимпиада.. 1997 |
|
|
Найдите все пары целых чисел (x,y), удовлетворяющих уравнению 1 + 1996x + 1998y = xy.
Задача 2:Внутри равностороннего треугольника ABC взята точка M. D, E и F – основания перпендикуляров, опущенных из M на стороны BC, CA и AB соответственно. Найдите геометрическое место точек M, дл которых угол FDE прямой.
Задача 3:Найдите все многочлены p(x) удовлетворяющие для любого x следующему уравнению: (x – 16)p(2x) = 16(x – 1)p(x).
Задача 4:a,b и c – неотрицательные вещественные числа. Докажите, что если a + b + c ≥ abc, то a² + b² + c² ≥ abc.
Задача 5:S – множество всех нечетных целых чисел больших 1. Для каждого x из S через δ (x) обозначим такое целое число, что 2 δ (x) < x < 2 δ (x) + 1. Для a,b из S определим a*b следующим образом: a*b = 2 δ (a) – 1(b – 3) + a. Вычислим, например, 7*5. δ (7) = 2, значит 7*5 = 22 – 1(5 – 3) + 7 = 11 (в то же врем 5*7 = 22 – 1(7 – 3) + 5 = 13).Докажите, что если a,b,c из S, то
Для положительного числа n через σ (n) обозначим сумму всех положительных делителей n. Например, σ (3) = 1 + 3 = 4, σ (6) = 1 + 2 + 3 + 6 = 12. Число a называется избыточным, если σ (a) > 2a. Докажите, что произведение избыточного числа на любое натуральное – избыточное число.
Задача 7:В четырехугольник ABCD вписана окружность. ∠ A = ∠ B = 120, ∠ D = 90, |BC| = 1. Найдите длину стороны AD.
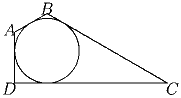
A – подмножество 0,1,2,3, … ,1997 содержащее не менее 1000 элементов. Докажите, что либо A содержит некоторую степень двойки, либо в A найдутся два различных числа a и b таких, что a + b степень двойки.
Задача 9:S – множество всех натуральных чисел n, удовлетворяющих следующим условиям:
p – простое число большее 2, n – натуральное число и T = 1,2, … ,n. Число n назовем p-делимым, если существуют непустые T1, T2,…, Tp подмножества T такие, что
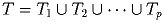 ;
;
| Задачная база >> Национальные зарубежные олимпиады >> Ирландия >> 1997 | Убрать решения |