 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Ирландия >> 1999 | Убрать решения |
|
|
| Ирландская математическая олимпиада.. 1999 |
|
|
Найдите все вещественные x, удовлетворяющие неравенству
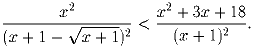
Докажите, что существует число Фибоначчи, которое делится на 1000.
Задача 3:В треугольнике ABC проведены высота AD, биссектриса BE и медиана CF. Докажите, что эти отрезки пересекаются в одной точке тогда и только тогда, когда a²(a – c) = (b² – c²)(a + c), где a,b,c – длины сторон BC, AC и AB соответственно.
Задача 4:Докажите, что квадрат 100 × 100 с вырезанным из центра квадратом 2 × 2 можно разрезать на прямоугольники 1 × 3, а если квадрат 2 × 2 был вырезан из угла доски, то остаток разрезать на такие прямоугольники невозвможно.
Задача 5:
Последовательность un строится следующим образом: u0 = 0, u1 = 1, а un + 1 – наименьшее натуральное число, большее un, которое не образующет арифметической прогрессии ни с какими двум элементами u0,u1, … ,un. Найдите u100.
Задача 6:Решите систему уравнений:
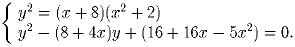
Мультипликативная функция f удовлетворяет условию f(p + q) = f(p) + f(q) для простых p и q. Докажите, что f(2) = 2, f(3) = 3 и f(1999) = 1999.
Задача 8:
a,b,c,d – положительные числа с суммой 1. Докажите, что
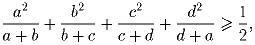
Задача 9:
Найдите все натуральные числа m равные четвертой степени количества своих натуральных делителей.
Задача 10:
ABCDEF – выпуклый шестиугольник, в котором AB = BC, CD = DE, EF = FA и ∠ ABC + ∠ CDE + ∠ EFA = 360. Докажите, что перпендикуляры, опущенные из вершин A, B и C на FB, BD и DF соответственно, пересекаются в одной точке.
| Задачная база >> Национальные зарубежные олимпиады >> Ирландия >> 1999 | Убрать решения |