 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Италия >> 1995 | Убрать решения |
|
|
| Итальянская математическая олимпиада.. 1995 |
|
|
Найдите все n при которых квадрат n × n можно разрезать на фигурки 1pt

Задача 2:
В классе 20 учеников прошло два экзамена. Ученик A умнее ученика B если его баллы за оба экзамена больше соответствующих баллов второго. Оценка за экзамен – натуральное число от 1 до 10. a) Докажите, что найдутся три ученика такие, что первый умнее второго, а второй – умнее третьего. b) Нашлись бы такие три человека, если в классе было бы 19 учеников?
Задача 3:
В точке A находится человек. В каждый момент времени он с равной вероятностью переходит в любую соседнюю вершину. a) Найдите вероятность того, что через 4 перехода человек окажется в точке C. b) Найдите точку, в которой человек окажется через n переходов с наибольшей вероятностью (n > 4).
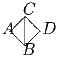
Задача 4:
O – центр окружности, описанной около остроугольного треугольника ABC. AD – биссектриса. Перпендикуляр, опущенный из точки D на прямую AO пересекает прямую AC в точке P, принадлежащей отрезку AC. Докажите, что AB = AP.
Задача 5:
Две не лежащие в одной плоскости окружности касаются друг друга и имеют общую касательную в этой точке. Докажите, что они лежат на поверхности одной сферы.
Задача 6:
Найдите все натуральные x и y для которых x² + 615 = 2y.
Решение:
Рассматривая остатки при делении на 3 получаем, что y – четное. Пусть y = 2t, тогда 22t = x² + 615 и (2t – x)(2t + x) = 615 = 3 • 5 • 41. Осталось представить 615 в виде произведения двух множителей сумма которых равна степени 2, что можно сделать единственным образом – 615 = 123 × 5, откуда t = 6, x = 59, y = 12.
| Задачная база >> Национальные зарубежные олимпиады >> Италия >> 1995 | Убрать решения |